Science 1 Physics

Assignment 1 (17 Sep 2009) SOLUTIONS

(Turn in Mon 21 Sep)

"Waves II "

Work through problems 32, 34, 46 & 50 from Knight, Ch. 21.

and

Write a sentence describing what is hardest about the 2nd half of the chapter.

Obviously there is no "correct answer" for this sentence. We were just trying to find out what gave you the most trouble.



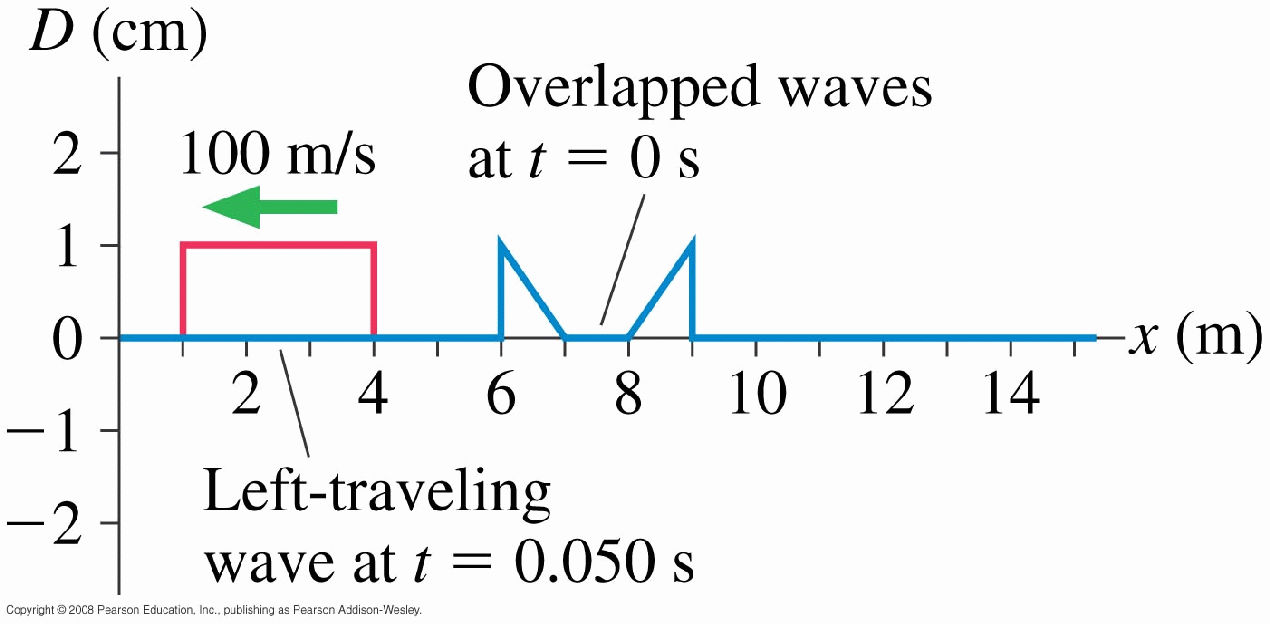
32: Two waves on a string travel in opposite directions at 100 m/s. The figure shows a snapshot graph of the string at t = 0, when the two pulses overlap, and another snapshop graph of the left-going pulse at t = 0.050 s. Draw a snapshot graph of the right-going pulse at t = 0.050 s.



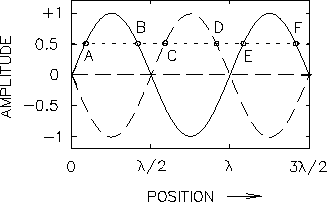
34: A string vibrates at its third-harmonic frequency. The amplitude at a point 30 cm from one end is half the maximum amplitude. How long is the string?

We naturally assume that both ends of the string are fixed, so that the ends are nodes (zero amplitude & zero phase at x = 0). The amplitude is 1/2 its maximum value when sin(k x) = 0.5, i.e. when k x = /6 = 30o or /6 + any integer multiple of . Thus for x = 0.3 m, we have the desired condition for (0.3 m) k = (n + 1/6) . Since k = 2/, this implies = (0.6 m)/(n + 1/6). The string is vibrating at its third-harmonic frequency, meaning that there are two nodes and three half-wavelengths between the ends, or that the length of the string is L = 3 /2, or = 2L/3 = (0.6 m)/(n + 1/6). Simplifying, we have L = (0.9 m)/(n + 1/6). The simplest case is of course for n = 0, giving L0 = 5.4 m (for point A); the next possibility (for n = 1) is L1 = 0.77142857 m (for point C); for n = 2 we get L2 = 0.41538462 m (for point E); and so on. Cool, huh?

But this is wrong! For one thing, n can't be bigger than 2, because there are only three half-wavelengths (and therefore three half-periods) available. For another thing, there are also points B, D and F, corresponding to the positions coming back from the "far end". Any one of these points could be 30 cm from the left end, giving a different overall length in each case. Several people recognized that there is more than one answer to this question, but only one [not me!] saw that there were exactly six!



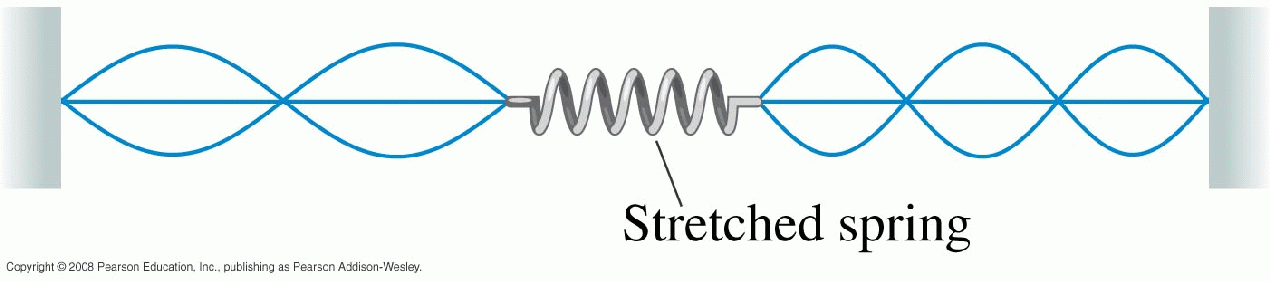
46: The two strings are of equal length and are being driven at equal frequencies. The linear density of the left string is 2.0 g/m. What is the linear density of the right string?



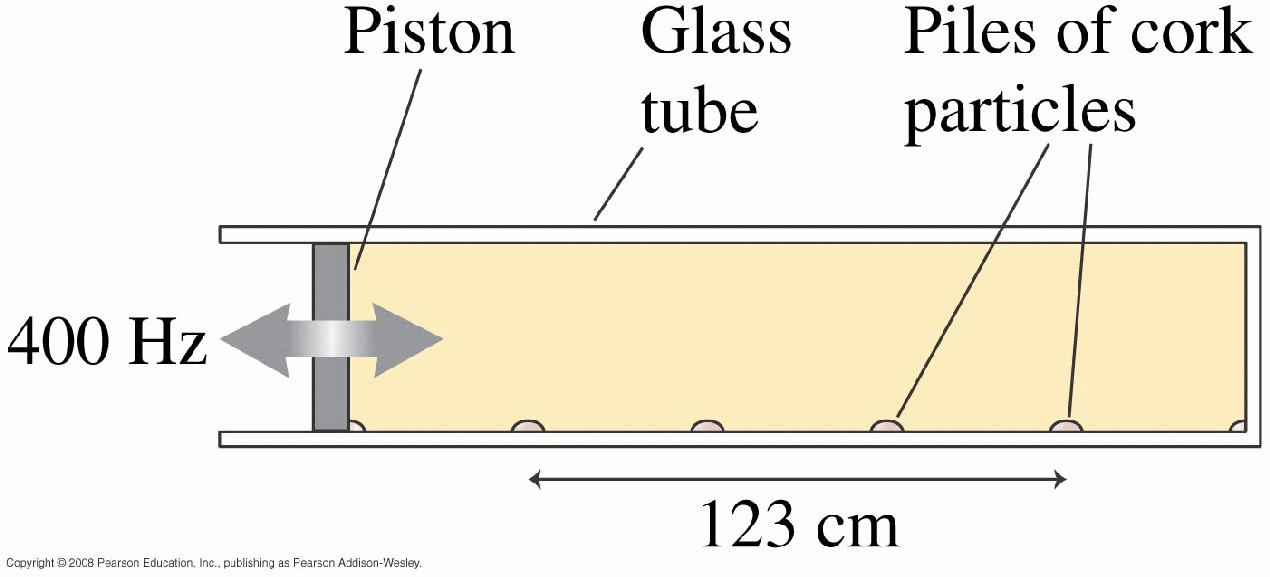
50: The tube is filled with pure oxygen and the piston is driven at 400 Hz. What is the speed of sound in oxygen?

Jess H. Brewer - Last modified: Thu Sep 24 22:04:34 PDT 2009