Sunday 04 Oct 2009, aboard the MV Frances Barkley
You have read chapters on, heard lectures about, and seen lots of cool computer simulations of waves. Now you're going to observe, analyze and discuss the real thing.On the boat trip home from Bamfield (and, for extra credit, on the ferry ride back to Vancouver) you should record your observations, measurements and estimates as described below, discuss them with your classmates (form groups for this purpose, as usual) and reach tentative interpretations and/or conclusions about the WAVES IN A BOAT'S WAKE.
When you get home, get some sleep! Rest up for Monday. Then (on Monday) write up a short report (preferably in LATEX)1 summarizing this exercise to hand in by Tuesday morning before class. 0.6 m/s);
but that too was fraught with opportunities for error,
like trying to read distances off Google Maps.
0.6 m/s);
but that too was fraught with opportunities for error,
like trying to read distances off Google Maps.
Although the "vee" is less well defined
in some of the other pictures, it is striking that
the opening angle of the "vee" is about the same in all cases,
whether the wave is caused by a small, planing speedboat
or a large, lumbering ship.
This "vee" pattern is know as the
"Kelvin wake"
after Lord Kelvin [the same guy that Physicists'
favourite kind of "degrees" are named after],
who first recorded and explained them.
The crests of the "wavelets" in the Kelvin wake
make an angle of about 53o with the boat's path. The
Wikipedia
article explains why.
Inside the "vee" there are still smaller (shorter-wavelength) wavelets
whose direction of propagation is more nearly perpendicular
(crests more nearly parallel) to the boat's velocity.
The still pictures don't reveal the fact
(which almost everyone noticed) that the wave patterns
remain in the same position relative to the ship.
That is, all the waves "keep pace" with the ship,
even though waves of different wavelengths
move at different speeds through the water.
The shorter-wavelength waves move slower.
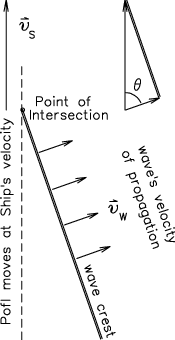
So how do slower waves "keep pace" with the ship?
By propagating at a large angle to the ship's direction!
This seems counterintuitive until you think about
what it means for a wave to "keep up": it must have a crest
meeting the ship in the same place all the time.
Imagine sweeping a flashlight beam along a wall at night:
when the beam hits the wall at right angles, the beam spot
moves slowly; but as the angle grows, so does the apparent
speed of the beam spot, although the light itself
always travels at the same speed.
It is the phase velocity you see "moving" along the wall;
nothing is actually propagating at that speed.
So wake waves whose crests are almost parallel
to the boat's direction don't have to move as fast
to keep their phase with the boat.
Here is a diagram to help you visualize this
(a movie would of course be better):

 5.5
5.5 0.6 m/s for a wavelength of
around 6
0.6 m/s for a wavelength of
around 6 2 m.
The wavelength of the "wavelets" in the Kelvin wake
behind the Frances Barkley looks to be about
1.6
2 m.
The wavelength of the "wavelets" in the Kelvin wake
behind the Frances Barkley looks to be about
1.6 0.4 m. These only have to propagate
at (5.5
0.4 m. These only have to propagate
at (5.5 0.6 m/s) cos(53o)
= 3.3
0.6 m/s) cos(53o)
= 3.3 0.4 m/s to keep in phase with the boat.
0.4 m/s to keep in phase with the boat.
 2 m
propagating at a speed of about 5.5
2 m
propagating at a speed of about 5.5 0.6 m/s
and a Kelvin wavelet of wavelength 1.6
0.6 m/s
and a Kelvin wavelet of wavelength 1.6 0.4 m
propagating at a speed of about 3.3
0.4 m
propagating at a speed of about 3.3 0.4 m/s.
The approximate dispersion relation for deep-water waves is
supposed to be v
0.4 m/s.
The approximate dispersion relation for deep-water waves is
supposed to be v 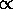
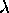 1/2.
Do our observations agree with this prediction?
We should have v1/v2 =
(5.5
1/2.
Do our observations agree with this prediction?
We should have v1/v2 =
(5.5 0.6 m/s)/(3.3
0.6 m/s)/(3.3 0.4 m/s)
0.4 m/s)
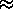 1.7
1.7 0.3
= (
0.3
= (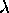 1 /
1 /
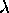 2)1/2
= [(6
2)1/2
= [(6 2 m)/(1.6
2 m)/(1.6 0.4 m)]1/2
= [3.8
0.4 m)]1/2
= [3.8 1.5]1/2 = 1.9
1.5]1/2 = 1.9 0.8,
so we have agreement within our uncertainty,
which is as good as it gets in experimental science.
(Of course, things get more interesting when we
work harder to make the uncertainties smaller;
that's the essence of experimental science.)
0.8,
so we have agreement within our uncertainty,
which is as good as it gets in experimental science.
(Of course, things get more interesting when we
work harder to make the uncertainties smaller;
that's the essence of experimental science.)
Needless to say, I did not expect this detailed a report
from each person or group; your task was to make empirical
observations of a complex phenomenon with only rudimentary
theoretical prejudices. It was a test of your ability to
observe objectively and report honestly - an essential skill
for any scientist, and one which is too often suppressed
by "canned" exercises with well-defined "right answers"
(or by the promise of fame and fortune if your result
agrees with an exciting theoretical prediction - professional
scientists are just as vulnerable to this temptation as students).
I was generally pleased with your results!
Site maintained by
Jess H. Brewer -
Last modified: Thu Oct 15 22:19:25 PDT 2009