- . . . system1
- Only the next-to-last answer is correct.
The last one would be right if one of the ``increases''
were a ``decreases'' but the derivative defines 1/T, not T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . target?2
- Along
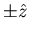 the magnetic field has no effect
so it is easy to hit the target; along any of the other directions,
the radius of curvature of the beam's path is r = p/qB
and so the maximum distance the beam ever gets from the ``gun''
is 2r (the diameter of its orbit) which is less than the
distance to the target. It would be hard to aim a curving
beam anyway.
the magnetic field has no effect
so it is easy to hit the target; along any of the other directions,
the radius of curvature of the beam's path is r = p/qB
and so the maximum distance the beam ever gets from the ``gun''
is 2r (the diameter of its orbit) which is less than the
distance to the target. It would be hard to aim a curving
beam anyway.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . flow)3
- This is an essay question; there are an infinite number
of ways to answer it correctly . . . or incorrectly.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . answer.4
- Zero. The net charge enclosed in the cube is zero,
so Gauss' Law says the net flux of electric field out of the cube
is zero too. The average E is the net flux divided by the
area of the cube, thus also zero.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . closed.5
- Nothing. The capacitor already has the charge
the battery is capable of placing on it, so there is no
voltage across the resistor and no current flows.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . closed.6
- This time charge must flow through the resistor
to get onto the capacitor. It eventually ends up with
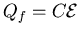 .
The charge builds up as
.
The charge builds up as
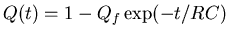 .
Putting in the numbers,
Qf = 10 C and the time constant RC = 100 s.
You can easily draw a sketch of Q(t).
.
Putting in the numbers,
Qf = 10 C and the time constant RC = 100 s.
You can easily draw a sketch of Q(t).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
 )7
)7
- Boltzmann showed that the probability a system being in
a state of energy
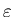 while in thermal equilibrium with
a heat reservoir at temperature
while in thermal equilibrium with
a heat reservoir at temperature 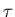 is proportional to
is proportional to
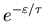 .
For the state with
zero energy this is just 1, so the relative probability
of being in the other state is just
.
For the state with
zero energy this is just 1, so the relative probability
of being in the other state is just
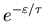 .
If we want this to equal e-1 we must have
.
If we want this to equal e-1 we must have
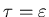 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . awake?8
- Following the same argument as before, we are looking for
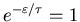 .
This is only true if
.
This is only true if
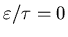 ,
which for finite
,
which for finite
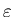 is only
true when
is only
true when
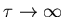 .
You don't really have to do the
mathematics to realize this, though, if you think about what
the Boltzmann distribution describes.
.
You don't really have to do the
mathematics to realize this, though, if you think about what
the Boltzmann distribution describes.
Anyone who got stuck on this part ought to have gotten a
good retroactive hint from the graphs in the next part!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
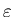 .9
.9
-
This is just an exponential decay from 1 at
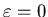 to zero as
to zero as
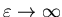 ,
with the 1/e point
at
,
with the 1/e point
at
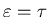 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
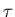 .10
.10
-
This is a little cuter: the value at
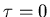 is zero;
it stays ``pretty small'' until it shoots up around
is zero;
it stays ``pretty small'' until it shoots up around
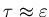 and then slowly approaches 1
as
and then slowly approaches 1
as
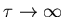 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . words.)11
- The magnetic field goes around the pipe in closed circles
as dictated by the right hand rule. Inside there is no field.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . Tesla).12
- Pick a circular Ampèrian loop of radius r
centred on the same axis as the pipe:
by symmetry, the field must be along the loop and
have the same strength at each point on the loop, so
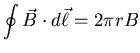 .
Inside the pipe (r < R) there is no current linking the loop
so B = 0. Outside the pipe (r > R) the whole current I
links the loop and so
.
Inside the pipe (r < R) there is no current linking the loop
so B = 0. Outside the pipe (r > R) the whole current I
links the loop and so
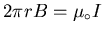 ,
giving
,
giving
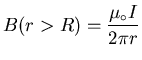 .
The field thus stays zero out to r=R and then jumps up to
.
The field thus stays zero out to r=R and then jumps up to
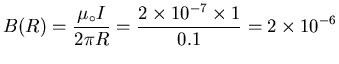 T.
From there on out,
T.
From there on out,
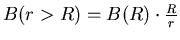 .
Easy to draw.
.
Easy to draw.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
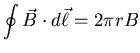 .
Inside the pipe (r < R) there is no current linking the loop
so B = 0. Outside the pipe (r > R) the whole current I
links the loop and so
.
Inside the pipe (r < R) there is no current linking the loop
so B = 0. Outside the pipe (r > R) the whole current I
links the loop and so
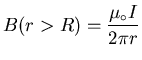 .
The field thus stays zero out to r=R and then jumps up to
.
The field thus stays zero out to r=R and then jumps up to
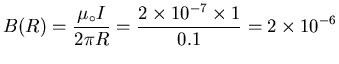 T.
From there on out,
T.
From there on out,