- . . . larger?1
-
At point A. (Twice as strong as at B.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . zero?2
-
Positive. You are moving ``against the field'' and hence ``uphill.''
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . B?3
-
Zero. If you come in along the vertical axis, the field is always
perpendicular to your motion and therefore does no work.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . given.4
-
If the plates carry a charge Q then the surface charge density is
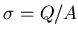 .
The field between the plates would thus be
.
The field between the plates would thus be
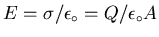 if the gap were empty.
The effect of the dielectric is to reduce E by a factor
if the gap were empty.
The effect of the dielectric is to reduce E by a factor
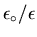 .
Thus in region 1 the field is
.
Thus in region 1 the field is
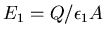 and in region 2 the field is
and in region 2 the field is
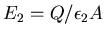 .
Moving from one plate to the other we travel a distance d/2
along E1 and another distance d/2 along E2
for a net potential change of
.
Moving from one plate to the other we travel a distance d/2
along E1 and another distance d/2 along E2
for a net potential change of
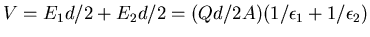 .
Since C is defined by Q = CV or C = Q/V, we have
.
Since C is defined by Q = CV or C = Q/V, we have
![\fbox{ ${\displaystyle C = {2 A \over \left[
{1 \over \epsilon_1} + {1 \over \epsilon_2} \right] d } }$\space }](img11.gif) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
 ?5
?5
-
I.e. what is the time constant
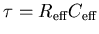 of this circuit?
of this circuit?
By symmetry the same charge must flow through each
of the resistors onto each of the capacitors. The three resistors
in the lower left corner are thus in parallel and have an effective
resistance of 1/3 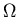 ;
similarly for the three resistors in the
upper right corner. These two effective resistors are in series,
giving an overall
;
similarly for the three resistors in the
upper right corner. These two effective resistors are in series,
giving an overall
 = 2/3
= 2/3 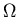 .
By similar logic, the capacitors are all in parallel, giving immediately
.
By similar logic, the capacitors are all in parallel, giving immediately
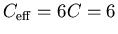 F. Thus
F. Thus
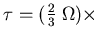 6 F)
or
6 F)
or
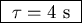 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . diagram.6
-
3.0in
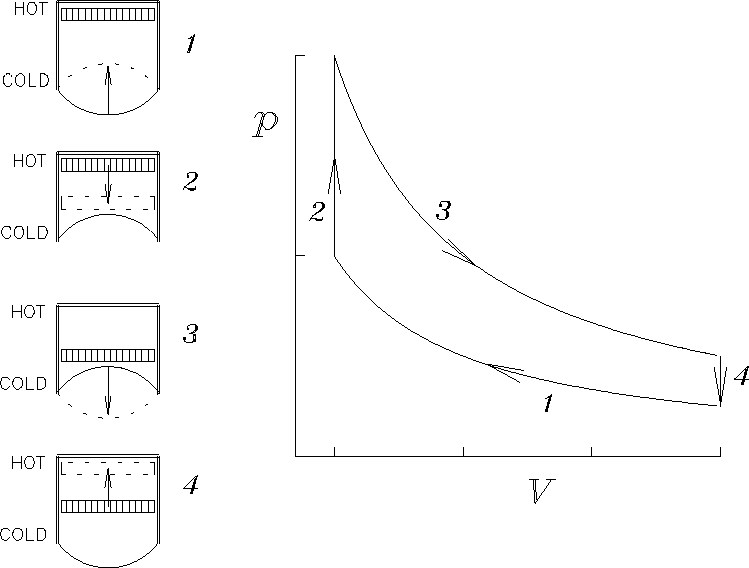
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . refrigerator?7
-
An engine. More work (
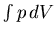 )
is done by the gas
in the expansion (3) at high temperature
than is done on the gas
in the compression (1) at low temperature.
No work is done in steps 2 and 4.
)
is done by the gas
in the expansion (3) at high temperature
than is done on the gas
in the compression (1) at low temperature.
No work is done in steps 2 and 4.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . Earth.8
-
A charge Q will distribute itself uniformly over the surface
of a conducting spherical shell (all the charges try to get
as far away from each other as possible).
The resultant charge distribution has spherical symmetry,
giving an isotropic radial electric field (outside the sphere)
that is just like that from a point source.
The electrostatic potential (relative to any point at infinite distance)
is therefore
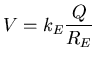 .
The capacitance C = Q/V is therefore
.
The capacitance C = Q/V is therefore
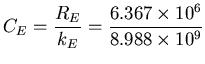 or
or
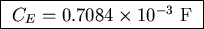 .
(Pretty small, when you consider that you can buy
a 5 F capacitor that fits in the palm of your hand!)
.
(Pretty small, when you consider that you can buy
a 5 F capacitor that fits in the palm of your hand!)
(This is really a ``Quickie'' with numbers, meant as a gift.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . ).9
-
GAUSS' LAW can be combined with cylindrical symmetry
to show first that
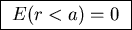 (there is no charge
enclosed within a cylindrical surface whose radius is less that a).
Next consider r>b: all the charge in a segment
of length L is enclosed within a cylindrical surface of radius
r>b, so the result is the same as for a line of charge:
(there is no charge
enclosed within a cylindrical surface whose radius is less that a).
Next consider r>b: all the charge in a segment
of length L is enclosed within a cylindrical surface of radius
r>b, so the result is the same as for a line of charge:
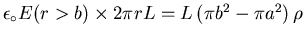 or
or
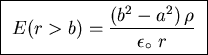 .
Finally, for a<r<b the enclosed charge in a segment
of length L is
.
Finally, for a<r<b the enclosed charge in a segment
of length L is
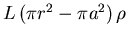 ,
giving
,
giving
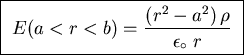 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![\fbox{ ${\displaystyle C = {2 A \over \left[
{1 \over \epsilon_1} + {1 \over \epsilon_2} \right] d } }$\space }](img11.gif) .
.
![]() ;
similarly for the three resistors in the
upper right corner. These two effective resistors are in series,
giving an overall
;
similarly for the three resistors in the
upper right corner. These two effective resistors are in series,
giving an overall
![]() = 2/3
= 2/3 ![]() .
By similar logic, the capacitors are all in parallel, giving immediately
.
By similar logic, the capacitors are all in parallel, giving immediately
![]() F. Thus
F. Thus
![]() 6 F)
or
6 F)
or
![]() .
.
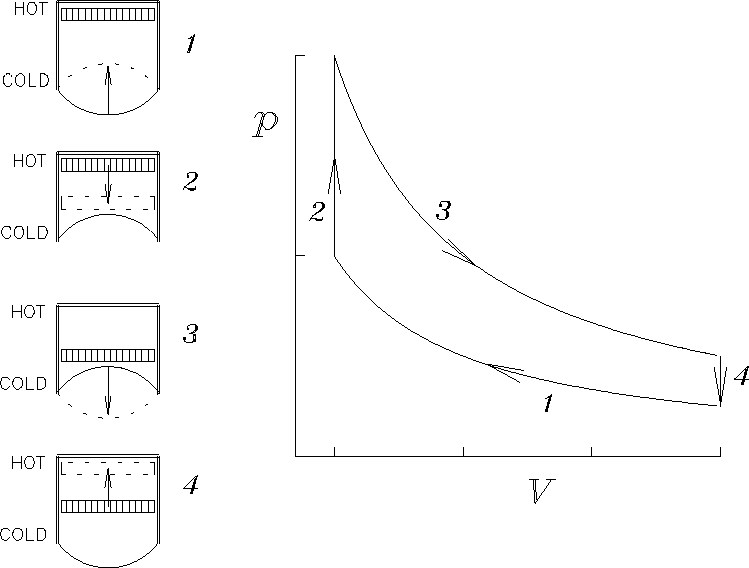
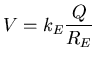 .
The capacitance C = Q/V is therefore
.
The capacitance C = Q/V is therefore
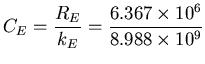 or
or
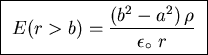 .
Finally, for a<r<b the enclosed charge in a segment
of length L is
.
Finally, for a<r<b the enclosed charge in a segment
of length L is
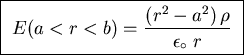 .
.