- (a)
- Shown below are six graphs describing the motion of
two different objects, A and B, in one dimension.
The horizontal axis is the same for each graph
and represents time over the range from 0 to 2 s.
The vertical axes are either distance x
[in m], speed v [in m/s]
or acceleration a [in m/s2],
with only the numerical values indicated.
There is one and only one graph of each of x(t), v(t) and a(t)
for each of the two objects.
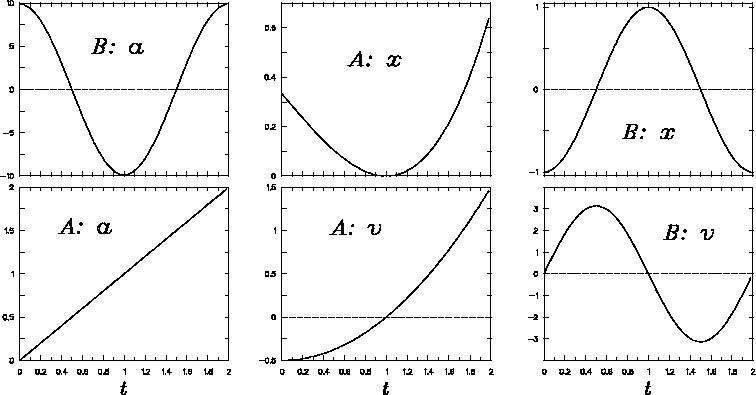
- i.
- Which is which? Indicate on each graph which function it describes for which object [e.g. ``A: v(t)'']. One graph is already labelled with an A to get you started. ANSWER: See graph.
- ii.
- Describe the motion of both A and B
in words. (No numbers or algebraic symbols!)
ANSWER: The acceleration of A increases linearly with time.
(This is known as ``constant jerk''.)
Its initial acceleration is zero, its initial velocity is negative
and its initial position is positive; thus it initially moves back
toward the origin, which it reaches after one second, and then
turns around and accelerates away again.
The motion of B should be immediately recognized as SHM; it remains only to define the period (two seconds), the amplitude (one meter) and the initial phase (pi). Remember, each time you take a derivative (e.g. to get the velocity or the acceleration) you multiply by the frequency, which is larger than unity, so the smallest vertical excursions must be for the displacement itself.
- (b)
- What is the orbital radius of a geosynchronous satellite
(one which is always directly over the same point on the Earth's equator)?
ANSWER: The FBD for the satellite is trivial: there is a single force
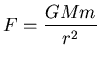 acting to cause a
centripetal acceleration of
acting to cause a
centripetal acceleration of
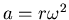 ;
Newton's Second Law
thus demands
;
Newton's Second Law
thus demands
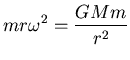 or
or
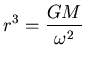 .
Since
.
Since
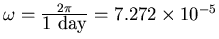 s-1, plugging in
G and M from the constants provided gives
s-1, plugging in
G and M from the constants provided gives
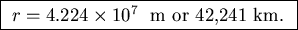
For some reason lots of people felt the Earth's radius should be subtracted from this value.
Quite a few people used one year as the orbital period. ?!
Others calculated the velocity and centripetal acceleration of a point on the Earth's surface for some reason.
- (c)
- Suppose that a 100 W source radiates light of wavelength 600 nm
uniformly in all directions and that the eye can detect this light
if at least 20 photons per second enter a dark-adapted pupil
6 mm in diameter.
How far from the source can the light be detected by eye?
ANSWER: This question required that you remember one of the formulae for the energy of a photon, either E = h f (where f is the frequency in Hertz) or
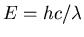 where
where 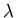 is
the wavelength of the light, c is the speed of light and h
is Planck's constant (provided on the last page). This was the
easy part, giving
is
the wavelength of the light, c is the speed of light and h
is Planck's constant (provided on the last page). This was the
easy part, giving
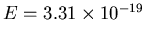 J and implying that
the source is emitting
J and implying that
the source is emitting
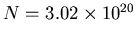 photons per second.
The harder part was then realizing that these N photons are
spread all over the surface of a sphere at radius R,
a total area of
photons per second.
The harder part was then realizing that these N photons are
spread all over the surface of a sphere at radius R,
a total area of 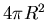 ,
of which only
,
of which only 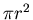 (where r = 0.003 m is the radius of the pupil)
is intercepted by the eye's pupil. Thus we want
(where r = 0.003 m is the radius of the pupil)
is intercepted by the eye's pupil. Thus we want
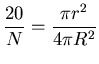 ,
which you can then solve for
,
which you can then solve for
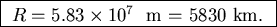
This was meant to be a conceptually challenging problem, but not a calculationally complex one. Hence its place in the ``Quickies'' section.
- (d)
- The positive muon (
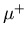 )
is an unstable elementary particle
with a constant decay rate of
)
is an unstable elementary particle
with a constant decay rate of
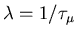 ,
where
,
where
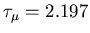
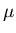 s is the mean muon lifetime.
The M15 muon beam at TRIUMF deposits an average of 106
positive muons in a target every second.
s is the mean muon lifetime.
The M15 muon beam at TRIUMF deposits an average of 106
positive muons in a target every second.
- i.
- What is the average number of these muons present
in the target at any time?
ANSWER: Again this is a simple problem once you get the idea, but many didn't. In steady state (after the beam has been going for a long time compared to microseconds) the number N0 of muons present in the target is (on average) constant. Thus dN/dt = 0 when N = N0. But a simple Chemistry-style rate equation says
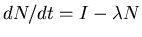 where I = 106 s-1 is the rate
at which muons are supplied by the beam. So in steady state
we must have
where I = 106 s-1 is the rate
at which muons are supplied by the beam. So in steady state
we must have
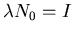 or
or
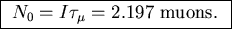
For some reason a few people thought it didn't make sense to have a non-integer number of muons on average, so they rounded down to 2. ??
- ii.
- If the beam is shut off suddenly at time t0, at what time is it most probable that there will be exactly one muon in the sample?
ANSWER: This part is just plain exponential decay:
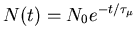 with
N0 = 2.197 and
the given value of
with
N0 = 2.197 and
the given value of 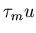 .
It's simplest to leave
times in microseconds for this part. Thus
to get N=1 we set
1 = 2.197 e-t/2.197
and take the log of both sides, giving
.
It's simplest to leave
times in microseconds for this part. Thus
to get N=1 we set
1 = 2.197 e-t/2.197
and take the log of both sides, giving
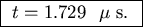
- (e)
- Which of the following features are essential for
SIMPLE HARMONIC MOTION?
A linear restoring force. Newton's First Law. .
.
Viscous damping. A quadratic potential minimum. A spring.
 .
A driving force at the resonant frequency.
.
A driving force at the resonant frequency.
- (a)
- Explain why this is so. Make your explanation simple and
qualitative but clear and complete enough to convince a skeptic.
A diagram may be very helpful, but numbers are irrelevant.
ANSWER: What matters here is whether there is any sudden acceleration of the end of the bat where you hold it. Call this point A and call the centre of mass C. The position of the ``sweet spot'' S is a distance x from A, whereas C is a distance L/2 from A for a uniform rod. The force F exerted by the ball on impact at S causes an acceleration of C given by ac = F/M where M is the mass of the bat. At the same time, F applied at S produces a torque
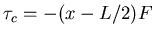 about the centre of mass.
This torque causes an angular acceleration
about the centre of mass.
This torque causes an angular acceleration
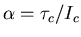 where
where
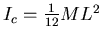 is the bat's moment of inertia
about its centre of mass. The net acceleration of point A
is the sum of the acceleration of C and the tangential
acceleration of A relative to C due to
is the bat's moment of inertia
about its centre of mass. The net acceleration of point A
is the sum of the acceleration of C and the tangential
acceleration of A relative to C due to 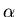 .
When these two exactly cancel, aA = 0 and there is
no ``jerk'' at A.
.
When these two exactly cancel, aA = 0 and there is
no ``jerk'' at A.
- (b)
- For an idealized ``stick bat'' (a thin, uniform rigid rod)
of length L, calculate the position of the ``sweet spot''
(assuming you can hold it by the very end).
ANSWER: Putting together the above equations gives
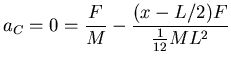 or
or
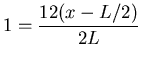 or
or
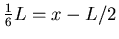 or
or
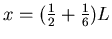 or
or
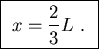
Several people guessed this answer. I gave some credit for good physical intuition.
This question was meant to be conceptually challenging, but it was surprising that only one person got it entirely right. Very few even saw the basic principle involved, demonstrating that an ability to reproduce a variety of practiced problem solutions is not the same as a real grasp of the principles of rigid body dynamics, which is necessary to solve even a simple problem of an unfamiliar type. This should not humiliate anyone, but rather give everyone a deeper respect for the subtlety of ``simple Mechanics''.
Another surprise was the number of people who evidently have never played any form of ball-and-bat game, and so had no physical intuition at all about the problem.
There were, as always, many who began hunting blindly for the right formula before asking, ``What's this really all about?'' You cannot do Physics this way. I hope this is now clear.
ANSWER: See sketch and FBD below. The box first slips
when the maximum acceleration of the platform is too large
to be transmitted to the box by the force of friction,
which has a maximum value of ![]() .
In SHM the
maximum acceleration is
.
In SHM the
maximum acceleration is
![]() ,
where A = 0.4 m
is the amplitude and
,
where A = 0.4 m
is the amplitude and
![]() s-1.
Thus in a few steps one obtains
s-1.
Thus in a few steps one obtains
![]() or
or
![]() or
or
![]() (One often hears that
(One often hears that
![]() ,
but if the box is glued
to the platform this is still physically realistic!)
,
but if the box is glued
to the platform this is still physically realistic!)
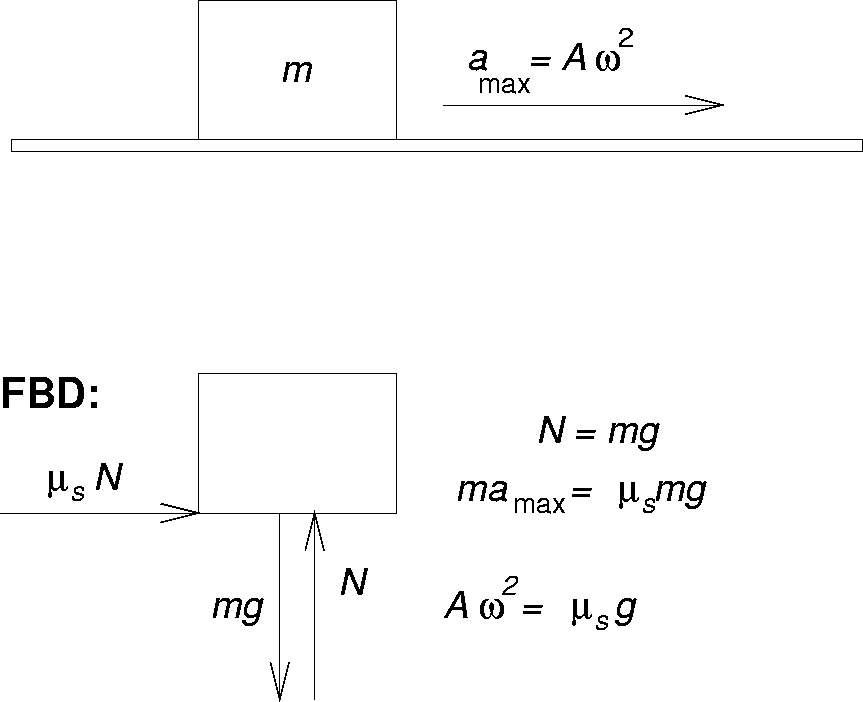
- (a)
-
A neutron is confined to a one-dimensional box
of length
L = 10-13 m.
Taking de Broglie's hypothesis into account,
what is the lowest kinetic energy it can have?
Express your answer in mega electron volts (MeV), where
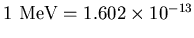 J.
J.
ANSWER: The state with the lowest kinetic energy K is the one with the lowest momentum p, which (by de Broglie's formula) is the one with the longest wavelength
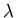 .
The longest wavelength one can fit into a box of length L
and still get the required nodes at the endpoints
is
.
The longest wavelength one can fit into a box of length L
and still get the required nodes at the endpoints
is
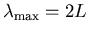 ,
giving
,
giving
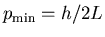 and
and
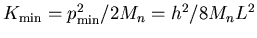 .
Plugging in
.
Plugging in
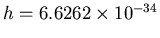 J-s,
J-s,
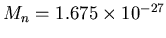 kg and
L = 10-13 m
gives
kg and
L = 10-13 m
gives
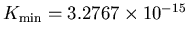 J or
J or
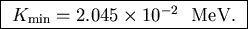
- (b)
-
What happens to the neutron's energy if L
shrinks by a factor of ten?
(This is about the size of a large atomic nucleus.)ANSWER: If
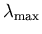 is 10 times smaller,
is 10 times smaller,
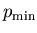 is 10 times bigger and
is 10 times bigger and
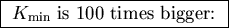 now
now
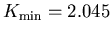 MeV.
MeV.
- (c)
-
What can you conclude about the typical binding energy
of a neutron in a nucleus?
ANSWER: If the binding energy were not of the order of
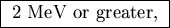 then the neutron would have enough
kinetic energy to escape, just from the effect of confinement.
This result is off by a factor on the order of 2 or 3 for
real nuclei, partly because of the 3-dimensional nature of
the ``box'' and partly because the potential created by the
strong interaction is not a square well but has ``soft sides''
allowing the neutron to spread out a bit extra. However,
very large nuclei are indeed unstable against the loss of
neutrons and protons, a topic to be studied at TRIUMF's new
ISAC facility!
then the neutron would have enough
kinetic energy to escape, just from the effect of confinement.
This result is off by a factor on the order of 2 or 3 for
real nuclei, partly because of the 3-dimensional nature of
the ``box'' and partly because the potential created by the
strong interaction is not a square well but has ``soft sides''
allowing the neutron to spread out a bit extra. However,
very large nuclei are indeed unstable against the loss of
neutrons and protons, a topic to be studied at TRIUMF's new
ISAC facility!
- (a)
- Sketch the intensity on the screen as a function of
the sine of the angle from the centre.
ANSWER:
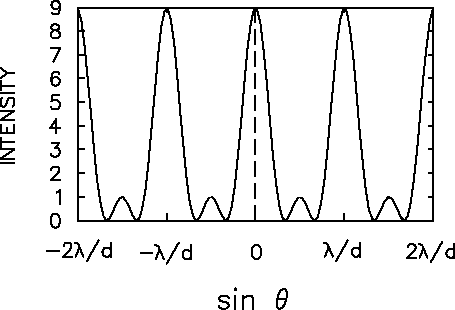
- (b)
- Give an expression for the angular positions of
the principal interference maxima.
ANSWER:
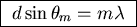
- (c)
- Give an expression for
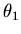 ,
the smallest angle
at which the intensity is zero.
,
the smallest angle
at which the intensity is zero.
ANSWER:
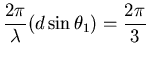
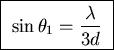
- (d)
- Draw a phasor diagram describing what happens at
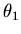 .
ANSWER:
.
ANSWER: