OPERATORS: (these all operate to the right)
![]() = partial derivative operator
as in
= partial derivative operator
as in
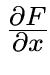 .
.
![]() = gradient operator:
= gradient operator:
![]()
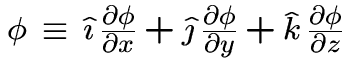
![]() = integral operator
as in
= integral operator
as in
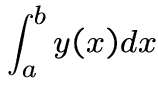
LOGICAL SYMBOLS: (handy shorthand)
![]() " . . . is defined to be . . . " (see above)
" . . . is defined to be . . . " (see above)
...
"Therefore . . . "
![]() " . . . implies . . . "
" . . . implies . . . "
![]() "there exists . . . "
"there exists . . . "
![]() " . . . such that . . . "
" . . . such that . . . "
/ [a slash through any logical symbol]
denotes negation
(e.g.
![]() " . . . does not imply . . . ")
" . . . does not imply . . . ")