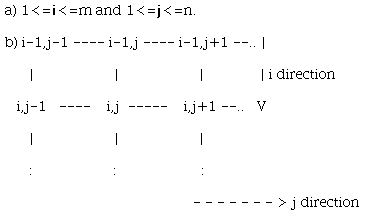
surf - 3D surface plot
surf draws a colored parametric surface using a rectangular grid defined by X and Y coordinates (if {X,Y} are not specified, this grid is determined using the dimensions of the Z matrix) ; at each point of this grid, a Z coordinate is given using the Z matrix (only obligatory data). surf has been created to better handle Matlab syntax. To improve graphical compatibility, Matlab users should use surf (rather than plot3d ).
Data entry specification :
In this paragraph and to be more clear, we won't mention GlobalProperty optional arguments as they do not interfer with entry data (except for "Xdata" , "Ydata" and "Zdata" property, see GlobalProperty ). It is assumed that all those optional arguments could be present too.
If Z is the only matrix specified, surf(Z) plots the matrix Z versus the grid defined by 1:size(Z,2) along the x axis and 1:size(Z,1) along the y axis.
If a {X,Y,Z} triplet is given, Z must be a matrix with size( Z )= [ m x n ], X or Y can be :
a) a vector : if X is a vector, length( X )= n . Respectively, if Y is a vector, length( Y )= m .
b) a matrix : in this case, size( X ) (or size( Y )) must equal size( Z ).
Color entry specification :
As stated before, the surface is created over a rectangular grid support. Let consider two independant variables i and j such as :
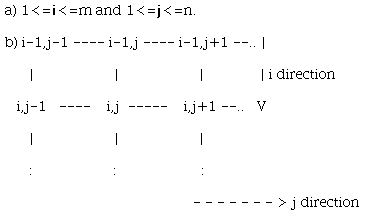
This imaginary rectangular grid is used to build the real surface support onto the XY plane. Indeed, X , Y and Z data have the same size (even if X or Y is vector, see below) and can be considered as 3 functions x(i,j) , y(i,j) and z(i,j) specifying the desired surface. If X or Y are vectors, they are internally treated to produce good matrices matching the Z matrix dimension (and the grid is forcibly a rectangular region).
Considering the 3 functions x(i,j) , y(i,j) and z(i,j) , the portion of surface defining between two consecutive i and j is called a patch.
By default, when no color matrix is added to a surf call, the color parameter is linked to the Z data. When a color matrix is given, it can be applied to the patch in two different ways : at the vertices or at the center of each patch.
That is why, if Z is a [ m x n ] matrix, the C color matrix dimension can be [ m x n ] (one color defined per vertex) or [ m-1 x n-1 ] (one color per patch).
Color representation also varies when specifying some GlobalPropery:
The FaceColor property sets the shading mode : it can be 'interp' or 'flat' (default mode). When 'interp' is selected, we perform a bilinear color interpolation onto the patch. If size( C ) equals size( Z )-1 (i.e. we provided only one color per patch) then the color of the vertices defining the patch is set to the given color of the patch.
When 'flat' (default mode) is enabled we use a color faceted representation (one color per patch). If size( C ) equals size( Z ) (i.e. we provided only one color per vertices), the last row and column of C are ignored.
The GlobalProperty arguments sould be used to customize the surface. Here is a brief description on how it works:
Note that all these properties can be (re-)set throught the surface entity properties (see surface_properties ).
By default, successive surface plots are superposed. To clear the previous plot, use clf() . To enable auto_clear mode as the default mode, edit your default axes doing:
da=gda();
da.auto_clear = 'on'
Enter the command surf to see a demo.
// Z initialisation
Z= [ 0.0001 0.0013 0.0053 -0.0299 -0.1809 -0.2465 -0.1100 -0.0168 -0.0008 -0.0000
0.0005 0.0089 0.0259 -0.3673 -1.8670 -2.4736 -1.0866 -0.1602 -0.0067 0.0000
0.0004 0.0214 0.1739 -0.3147 -4.0919 -6.4101 -2.7589 -0.2779 0.0131 0.0020
-0.0088 -0.0871 0.0364 1.8559 1.4995 -2.2171 -0.2729 0.8368 0.2016 0.0130
-0.0308 -0.4313 -1.7334 -0.1148 3.0731 0.4444 2.6145 2.4410 0.4877 0.0301
-0.0336 -0.4990 -2.3552 -2.1722 0.8856 -0.0531 2.6416 2.4064 0.4771 0.0294
-0.0137 -0.1967 -0.8083 0.2289 3.3983 3.1955 2.4338 1.2129 0.2108 0.0125
-0.0014 -0.0017 0.3189 2.7414 7.1622 7.1361 3.1242 0.6633 0.0674 0.0030
0.0002 0.0104 0.1733 1.0852 2.6741 2.6725 1.1119 0.1973 0.0152 0.0005
0.0000 0.0012 0.0183 0.1099 0.2684 0.2683 0.1107 0.0190 0.0014 0.0000];
//simple surface
surf(Z); // Note that X and Y are determined by Z dimensions
//same surface with red face color and blue edges
scf(2); // new figure number 2
surf(Z,'facecol','red','edgecol','blu")
// X and Y initialisation
// NB: here, X has the same lines and Y the same columns
X = [ -3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000
-3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000
-3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000
-3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000
-3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000
-3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000
-3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000
-3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000
-3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000
-3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000];
Y= [ -3.0000 -3.0000 -3.0000 -3.0000 -3.0000 -3.0000 -3.0000 -3.0000 -3.0000 -3.0000
-2.3333 -2.3333 -2.3333 -2.3333 -2.3333 -2.3333 -2.3333 -2.3333 -2.3333 -2.3333
-1.6667 -1.6667 -1.6667 -1.6667 -1.6667 -1.6667 -1.6667 -1.6667 -1.6667 -1.6667
-1.0000 -1.0000 -1.0000 -1.0000 -1.0000 -1.0000 -1.0000 -1.0000 -1.0000 -1.0000
-0.3333 -0.3333 -0.3333 -0.3333 -0.3333 -0.3333 -0.3333 -0.3333 -0.3333 -0.3333
0.3333 0.3333 0.3333 0.3333 0.3333 0.3333 0.3333 0.3333 0.3333 0.3333
1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
1.6667 1.6667 1.6667 1.6667 1.6667 1.6667 1.6667 1.6667 1.6667 1.6667
2.3333 2.3333 2.3333 2.3333 2.3333 2.3333 2.3333 2.3333 2.3333 2.3333
3.0000 3.0000 3.0000 3.0000 3.0000 3.0000 3.0000 3.0000 3.0000 3.0000];
// example 1
scf(3)
surf(X,Y,Z)
//example 2
// As you can see, the grid is not necessary rectangular
scf(4)
X(1,4) = -1.5;
Y(1,4) = -3.5;
Z(1,4) = -2;
surf(X,Y,Z)
// example 3
// X and Y are vectors => same behavior as sample 1
// With vectors, the grid is inevitably rectangular
scf(5)// new figure number 5
X=[ -3.0000 -2.3333 -1.6667 -1.0000 -0.3333 0.3333 1.0000 1.6667 2.3333 3.0000];
Y=X;
surf(X,Y,Z)
//LineSpec and GlobalProperty examples:
xdel(winsid()) // destroy all existing figures
surf(Z,Z+5) // color array specified
e=gce();
e.cdata_mapping='direct' // default is 'scaled' relative to the colormap
e.color_flag=3; // interpolated shading mode. The default is 4 ('flat' mode) for surf
scf(2)
surf(X,Y,Z,'colorda',ones(10,10),'edgeco','cya','marker','penta','markersiz',20,'markeredg','yel','ydata',56:65)
scf(3)
surf(Z,'cdatamapping','direct')
scf(4)
surf(Z,'facecol','interp') // interpolated shading mode (color_flag == 3)
scf(10)
axfig10=gca();
scf(11);
surf(axfig10,Z,'ydat',[100:109],'marker','d','markerfac','green','markeredg','yel') // draw onto the axe of figure 10
xdel(winsid())
plot2d , clf , xdel , delete , LineSpec , GlobalProperty ,
F.Leray