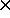 mean time between scattering
collisions
mean time between scattering
collisions 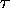 .
.
Drift velocity vd = acceleration (eE/m)
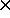 mean time between scattering
collisions
mean time between scattering
collisions 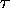 .
.
Problem: how can 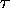 be
independent of the "steepness of the slope"?
Short excursion into Quantum Mechanics and Fermi-Dirac
statistics: electrons are fermions (half-integer spin)
so no two electrons can be in the same state. Thus the lowest
energy states are all full and the last electrons to go into a metal
occupy states with huge kinetic energies (for an electron) comparable
to 1 eV or 10,000 K. Only the electrons at this "Fermi level" can
change their states, so only they count in conduction. So our ideal
skiers actually have rocket-propelled skis and are randomly slamming
into trees (and each other) at orbital velocities (we will neglect the
problems of air friction); the tiny accumulated drift downhill is
imperceptible but it accounts for all conduction.
be
independent of the "steepness of the slope"?
Short excursion into Quantum Mechanics and Fermi-Dirac
statistics: electrons are fermions (half-integer spin)
so no two electrons can be in the same state. Thus the lowest
energy states are all full and the last electrons to go into a metal
occupy states with huge kinetic energies (for an electron) comparable
to 1 eV or 10,000 K. Only the electrons at this "Fermi level" can
change their states, so only they count in conduction. So our ideal
skiers actually have rocket-propelled skis and are randomly slamming
into trees (and each other) at orbital velocities (we will neglect the
problems of air friction); the tiny accumulated drift downhill is
imperceptible but it accounts for all conduction.
J = "flux" of charge = current per unit perpendicular area (show a "slab" of drifting charge) so J = n e vd, where n is number of charge carriers per unit volume. (For Cu, n is about 1029 m-3.)
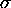 E,
defining the conductivity
E,
defining the conductivity
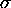 = n e2
= n e2
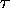 /m, measured in
Siemens per metre (S/m) if you like SI units (1 S = 1 A/V). I don't.
/m, measured in
Siemens per metre (S/m) if you like SI units (1 S = 1 A/V). I don't.
For Cu, 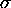 is around
108 S/m. Putting this together with n, e and
me = 9 x 10-31 kg, we get
is around
108 S/m. Putting this together with n, e and
me = 9 x 10-31 kg, we get
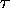 ~ 10-13 s.
At vF ~ 106 m/s this implies a
mean free path
~ 10-13 s.
At vF ~ 106 m/s this implies a
mean free path 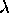 ~ 10-7 m. Compare lattice spacing ~ 10-10 m.
The drift velocity vd is only ~ 10-3 m/s.
~ 10-7 m. Compare lattice spacing ~ 10-10 m.
The drift velocity vd is only ~ 10-3 m/s.
In semiconductors, n is a factor of 10-7
smaller and vd is a factor of 107 larger,
almost as big as vF! So in some very pure
semiconductors transport is almost "ballistic", especially when the
size of the device is less than
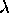 .
.
Briefly discuss superconductors.
The inverse of the conductivity is the resistivity
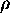 , measured in Ohm-meters.
(1 Ohm = 1 V/A).
, measured in Ohm-meters.
(1 Ohm = 1 V/A).
Use a cartoon of a cylindrical resistor of length L and
cross-sectional area A to explain how this works, giving
R = 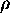 L/A
and the familiar V = I R.
L/A
and the familiar V = I R.
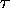 = RC.
= RC. Now do it mathematically: solve the differential equation for Q(t).
| "All points on a wavefront can be considered as point sources for the production of spherical secondary wavelets. At a later time, the new position of the wavefront will be the surface of tangency to these secondary wavelets." |
Less obvious is the fact that a wave also interferes with itself even if there is a continuous distribution of sources.
I = I0 sin2
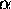 =
=  (a sin
(a sin
 /
/ ).
).
 =
=
a sin  1 =
1 =
 .
.
 equal to zero (condition
for an extremum). The resultant formula contains both a term
that goes to zero at the minima (zeroes) and another term
that reduces to
equal to zero (condition
for an extremum). The resultant formula contains both a term
that goes to zero at the minima (zeroes) and another term
that reduces to
| "All points on a wavefront can be considered as point sources for the production of spherical secondary wavelets. At a later time, the new position of the wavefront will be the surface of tangency to these secondary wavelets." |
Less obvious is the fact that a wave also interferes with itself even if there is a continuous distribution of sources.
I = I0 sin2
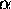 =
=  (a sin
(a sin
 /
/ ).
).
 =
=
a sin  1 =
1 =
 .
.
 equal to zero (condition
for an extremum). The resultant formula contains both a term
that goes to zero at the minima (zeroes) and another term
that reduces to
equal to zero (condition
for an extremum). The resultant formula contains both a term
that goes to zero at the minima (zeroes) and another term
that reduces to
a sin  1 =
1.22
1 =
1.22  .
.
Picture light shining through a large aperture and consider the region "straight ahead" of the aperture (i.e. neglect the fuzzy areas around the edges of the region in shadow).
If you place a small obstacle in the middle of the aperture, you are subtracting the amplitude contributions of the rays that would have arrived at the final screen from where the obstacle is now.
Now take away the obstacle and instead block off the whole aperture except for a hole of the same shape as the former obstacle (and in the same place). Now only the rays that were formerly being blocked are allowed through.
Since amplitudes are squared to get the intensity, a "negative" amplitude is just as good as a "positive" one. Thus the two situations give the same diffraction pattern on the final screen. There will be a bright spot directly behind the obstacle, just as you would expect for the hole.
The width of a diffraction pattern is defined as the angular distance from the central maximum to the first minimum.
Dm =
d m/d
m/d = m/d cos
= m/d cos
 m .
m .
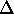
 )
can two colours be and still be resolved
by the grating?
)
can two colours be and still be resolved
by the grating?
Well, the two lines will just be resolved when the mth order principal maximum of one falls on top of the first minimum beyond the mth order principal maximum of the other.
By requiring the path length difference between
adjacent slits to differ (for the two colours) by
 /N
(where N is the number of slits) we ensure that the
phasor diagram for the second colour will just close
(giving a minimum) when that of the first colour
is a principal maximum. This gives a resolving power
/N
(where N is the number of slits) we ensure that the
phasor diagram for the second colour will just close
(giving a minimum) when that of the first colour
is a principal maximum. This gives a resolving power
Rm =
 /
/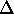
 = m N .
= m N .
Extend to more complex isotropic charge distributions.
.
.
.
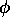 ["phi"] (chosen in class)
because HTML still has no Greek letters except "µ".
["phi"] (chosen in class)
because HTML still has no Greek letters except "µ".
In principle, it's easier to find E from V than vice versa, because it's a lot easier to integrate up a scalar function than a vector one! (And derivatives are easy, right?) However, in practice (at the level of P108) we are not going to be evaluating arbitrary, asymmetric charge distributions, but only the simple symmetric shapes and combinations thereof (using the principle of additive superposition). In these cases Gauss' Law allows us to find E easily and find V by simple integrations; so that's mostly what we do.
When you first encountered Algebra it gave you new powers -- now you could calculate stuff that was "magic" before. (Recall Clarke's Law.) This is what I call The Hammer of Math -- "When all you have is a hammer, everything looks like a nail."
This year (or maybe earlier) you have discovered that algebra is also a Door -- the door to another whole world of Math: the world of Calculus. Now you are exploring a new, different Hammer of Math -- the hammer of calculus, with which you can drive a whole new class of nails!
This cycle never ends, unless you give up and quit. Every year you will have a new Door of Math opened by the Hammer your mastered the year before. Next year you will probably go through the Door of Vector Calculus to find elegant and powerful Hammers for the nails of vector fields. I am not supposed to tell you about this, because it's supposed to be too hard. So I won't hold you responsible for this topic, but I gave you a handout on it (and will discuss it a little in class) because you deserve a glimpse of the road ahead. Think of it as a travel brochure that shows only the nice beaches and night clubs.
Topo maps and equipotentials: meaning of the gradient operator.
Thus Q = C V or V = (1/C) Q.
Units: a Farad (F) is one Coulomb per Volt.
Start with simplest (and most common) example,
the parallel plate capacitor: this case defines the terms
of reference clearly and is in fact a good approximation to most
actual capacitors. Know the formula by heart and
be able to derive it yourself from first principles!
The capacitance of a parallel plate capacitor of area A
with the plates separated by d is given by
Cpp =
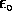 A/d.
A/d.
The capacitance of a capacitor consisting of
concentric spherical shells of radii a and b
is given by Csph =
4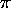
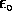 [(1/a) - (1/b)]-1.
[(1/a) - (1/b)]-1.
Capacitance of the Earth: treat the Earth as a conducting sphere of radius RE = 6.37 x 106 m. If the "other plate" is a concentric spherical conducting shell at infinite radius, what will be the potential difference between the "plates" when a charge of Q is moved from the shell at infinite radius to the Earth's surface? Answer: 710 µF (later on I will show you a capacitor you can hold in the palm of your hand that has a thousand times the capacitace of the Earth!) Note: this is not the same thing as you calculated in the 3rd homework assignment.
Pass around a 1 F capacitor -- more than 1000 times as big as the Earth!
The capacitance of a capacitor consisting of
concentric cylindrical shells of radii a and b
and equal length L is given by
Ccyl = 2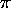
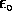 L/ln(b/a).
L/ln(b/a).
Note that in each case C = (numerical constant)
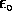 (distance).
Check that this makes dimensional sense.
(distance).
Check that this makes dimensional sense.
An array of capacitors in parallel has an equivalent capacitance equal to the sum of their separate capacitances. [Explain.]
An array of capacitors in series has an equivalent inverse capacitance equal to the sum of their separate inverse capacitances. [Explain.]
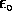 by
by  =
=

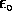 (where
(where  is the
dielectric constant, a pure number always
is the
dielectric constant, a pure number always
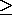 1)
and everything takes care of itself.
Thus C always gets bigger (by a factor of
1)
and everything takes care of itself.
Thus C always gets bigger (by a factor of
 )
when there is a dielectric in between the plates. [Explain.]
)
when there is a dielectric in between the plates. [Explain.]
The energy required to put a charge Q on a capacitor C is not just VQ! The first bit of charge goes on at zero voltage (no work) and the voltage (work per unit charge added) increases linearly with Q as the charge piles up: V = (1/C) Q. Thus dU = (1/C) Q dQ. Integrating yields U = (1/2C) Q2 or U = (1/2)C V2.
For a parallel plate capacitor, V = E d and
C = 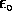 A / d.
Thus
U = (1/2)
A / d.
Thus
U = (1/2)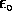 AE2 d. But A d is the
volume of the interior of the capacitor (the only place where
the electric field is nonzero). Thus if u is defined to be
the energy density per unit volume, then we have
u = (1/2)
AE2 d. But A d is the
volume of the interior of the capacitor (the only place where
the electric field is nonzero). Thus if u is defined to be
the energy density per unit volume, then we have
u = (1/2)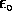 E2. "It turns out" that this prescription is
completely general! Wherever there is an electric field,
energy is stored at a density u given by the formula above.
E2. "It turns out" that this prescription is
completely general! Wherever there is an electric field,
energy is stored at a density u given by the formula above.
It is now getting really tempting to think of E as something "real", not just a mathematical abstraction.
Now reformulate in terms of the net magnetic flux
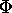 M = B L x
through the loop: V = B L dx/dt = -
d
M = B L x
through the loop: V = B L dx/dt = -
d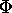 M/dt
(Faraday's Law).
M/dt
(Faraday's Law).
This also works for an arbitrary shaped loop, in which case V is the integral of E around the closed path (loop) enclosing the area through which the magnetic flux is changing.
Faraday's Law is more general than my derivation!
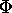 M?
M?
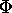 M = induced EMF.
M = induced EMF.
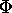 M = N A B (since B is uniform
inside and each field line links all N turns). Thus
M = N A B (since B is uniform
inside and each field line links all N turns). Thus 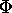 M = N A µ0 n I = L I if we define the
inductance of the solenoid to be L = A
µ0 N2/
M = N A µ0 n I = L I if we define the
inductance of the solenoid to be L = A
µ0 N2/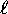 , where
, where 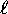 is the
actual length of the solenoid. This can also be written
L = µ0 n2
is the
actual length of the solenoid. This can also be written
L = µ0 n2
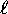 A. Note that
A. Note that
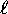 A is the volume
of the inside of the solenoid (where the field is).
A is the volume
of the inside of the solenoid (where the field is).
Similarly for the toroidal solenoid if it has a rectangular cross section so that integrating B over that area is easy:
Ltoroid = (µ0/2 ) N2h
log (b/a), where h is the height of the solenoid
and a & b are its inner & outer radii,
respectively.
) N2h
log (b/a), where h is the height of the solenoid
and a & b are its inner & outer radii,
respectively.
Note that in each case L has the form µ0 N2 x, where x is some length. Thus if L is measured in Henries [1 Henry = 1 Weber per Amp, where a Weber (1 Tesla metre2) is the unit of magnetic flux] then µ0 has units of Henries per metre.
Now some demonstrations:
In a long solenoid, I = B/µ0n and L is given above, so UL =
(1/2) (A µ0
n2 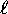 )
(B
)
(B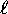 /µ0N)2
= (1/2µ0) B2 A
/µ0N)2
= (1/2µ0) B2 A 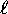 . But A
. But A 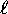 is just the volume of the interior of the
solenoid (where the field is), so the energy density per unit
volume stored in the solenoid is given by
umagn. = (1/2µ0)
B2.
is just the volume of the interior of the
solenoid (where the field is), so the energy density per unit
volume stored in the solenoid is given by
umagn. = (1/2µ0)
B2.
Like the analogous result for the energy density stored in an electric field, this result is completely general, far moreso than this example "derivation" justifies.
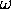 , where
, where
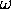 = (1/LC)-1/2.
= (1/LC)-1/2.
Go on from there . . . .
For each case, first picture the Mechanical analogue and then ask "What happens?" before launching into the mathematics.
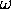 C and
XL =
C and
XL = 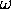 L
are the reactances of the capacitor and inductor,
respectively, and
L
are the reactances of the capacitor and inductor,
respectively, and 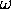 is the
driving frequency (in radians per second, don't forget!).
is the
driving frequency (in radians per second, don't forget!).  )
to defined the adjacent "wave front".
Naturally we make no attempt to draw 3D spherical waves
on a flat page;
all the 2D pictures are meant only as "conceptual shorthand".
This will be even more abstract as we start drawing "phasor"
diagrams.
)
to defined the adjacent "wave front".
Naturally we make no attempt to draw 3D spherical waves
on a flat page;
all the 2D pictures are meant only as "conceptual shorthand".
This will be even more abstract as we start drawing "phasor"
diagrams.
Be sure to review your trigonometry - we'll be using it!
The "near field" intensity pattern (where "rays" from the two sources, meeting at a common point, are not even approximately parallel) is difficult to calculate, though it is easy enough to describe how the calculation could be done. We will stay away from this region - far away, so that all the interfering rays may be considered parallel. Then it gets easy!
Simplified sketch assuming incident waves hitting the barrier
in phase (i.e. normal incidence) shows an obvious
path length difference of
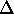
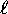 = d sin
= d sin  between the waves heading out from the two slits at that angle.
If this path length difference is an integer multiple
of the wavelength
between the waves heading out from the two slits at that angle.
If this path length difference is an integer multiple
of the wavelength
 we get constructive
interference. This defines the nth
Principal Maximum (PM):
we get constructive
interference. This defines the nth
Principal Maximum (PM):
d sin
 n =
n
n =
n 
 n
from the normal direction. We always define x = 0 to be
the position of the central maximum (CM) - i.e.
n
from the normal direction. We always define x = 0 to be
the position of the central maximum (CM) - i.e.
 = 0.
If the distance L from the slits to the screen is >> d
(the distance between the slits), as it almost always is, then
we can use the small angle approximations
sin
= 0.
If the distance L from the slits to the screen is >> d
(the distance between the slits), as it almost always is, then
we can use the small angle approximations
sin 
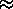 tan
tan 
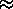
 so that
so that  n
n
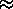 n
n
 /d
and xn = L tan
/d
and xn = L tan
 n
n
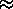 L
L
 n
giving xn
n
giving xn 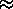 n L
n L  /d.
/d.
Be sure you can do calculations like these yourself. Such problems are almost always on the final exam.
Time permitting, I will start on Multiple Slit Interference. The handout covers this in detail; if I don't cover it today, be sure to study the handout over the weekend!
In this abstract world each wave is seen as an amplitude
Ai pointing away from some origin at a
phase angle 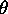 i
in "phase space" - a phasor. All the phasors representing
different wave amplitudes are "precessing" about the origin at a
common angular frequency
i
in "phase space" - a phasor. All the phasors representing
different wave amplitudes are "precessing" about the origin at a
common angular frequency 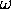 (the actual frequency of the waves) but their phase differences
do not change with time. Thus we can pick one wave arbitrarily to
have zero phase and "freeze frame" to show the angular orientations
(and lengths) of all the others relative to it.
(the actual frequency of the waves) but their phase differences
do not change with time. Thus we can pick one wave arbitrarily to
have zero phase and "freeze frame" to show the angular orientations
(and lengths) of all the others relative to it.
Phasors are vectors (albeit in a weird space) and so if they are to be added linearly we can construct a diagram for the resultant by drawing all the amplitudes "tip-to-tail" as for any vector addition. If there are any configurations that "close the polygon" (i.e. bring the tip of the last phasor right back to the tail of the first) then the net amplitude is zero and we have perfect destructive interference!
For an idealized case of N equal-amplitude waves
out of phase with their neighbours by an angle
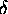 we will get a minimum when
N
we will get a minimum when
N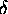 =
n(2
=
n(2 ),
satisfying the above criterion.
This is the condition for the nth minumum
of the N-slit interference pattern; we usually only care
about the first such minimum, which occurs where
N
),
satisfying the above criterion.
This is the condition for the nth minumum
of the N-slit interference pattern; we usually only care
about the first such minimum, which occurs where
N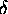 =
2
=
2 .
.
To see where in real space that first minimum occurs,
we have to go back to the origin of the phase differences
due to path length differences:
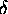 /2
/2 =
= 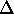
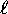 /
/ = d sin
= d sin
 /
/ ,
giving
,
giving
sin  first min. =
first min. =
 /N.
/N.
In this abstract world each wave is seen as an amplitude
Ai pointing away from some origin at a
phase angle 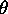 i
in "phase space" - a phasor. All the phasors representing
different wave amplitudes are "precessing" about the origin at a
common angular frequency
i
in "phase space" - a phasor. All the phasors representing
different wave amplitudes are "precessing" about the origin at a
common angular frequency 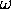 (the actual frequency of the waves) but their phase differences
do not change with time. Thus we can pick one wave arbitrarily to
have zero phase and "freeze frame" to show the angular orientations
(and lengths) of all the others relative to it.
(the actual frequency of the waves) but their phase differences
do not change with time. Thus we can pick one wave arbitrarily to
have zero phase and "freeze frame" to show the angular orientations
(and lengths) of all the others relative to it.
Phasors are vectors (albeit in a weird space) and so if they are to be added linearly we can construct a diagram for the resultant by drawing all the amplitudes "tip-to-tail" as for any vector addition. If there are any configurations that "close the polygon" (i.e. bring the tip of the last phasor right back to the tail of the first) then the net amplitude is zero and we have perfect destructive interference!
For an idealized case of N equal-amplitude waves
out of phase with their neighbours by an angle
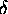 we will get a minimum when
N
we will get a minimum when
N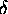 =
n(2
=
n(2 ),
satisfying the above criterion.
This is the condition for the nth minumum
of the N-slit interference pattern; we usually only care
about the first such minimum, which occurs where
N
),
satisfying the above criterion.
This is the condition for the nth minumum
of the N-slit interference pattern; we usually only care
about the first such minimum, which occurs where
N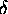 =
2
=
2 .
.
To see where in real space that first minimum occurs,
we have to go back to the origin of the phase differences
due to path length differences:
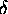 /2
/2 =
= 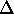
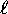 /
/ = d sin
= d sin
 /
/ ,
giving
,
giving
sin  first min. =
first min. =
 /N.
/N.
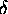 is another matter. It is shown in gory detail on the
Phasors handout and I will go over it in class,
but you will not be expected to derive it, nor would there be
many occasions when you would need to use it, as long
as you can reason out the positions of principal maxima and
secondary maxima or minima using the qualitative arguments
above. Nevertheless, it is nice to see a real derivation;
you may even wish to run the result through Mathematica
(or some other software package) to make nice plots of
"interference patterns" for your own amusement and the
edification of your friends.
is another matter. It is shown in gory detail on the
Phasors handout and I will go over it in class,
but you will not be expected to derive it, nor would there be
many occasions when you would need to use it, as long
as you can reason out the positions of principal maxima and
secondary maxima or minima using the qualitative arguments
above. Nevertheless, it is nice to see a real derivation;
you may even wish to run the result through Mathematica
(or some other software package) to make nice plots of
"interference patterns" for your own amusement and the
edification of your friends. Maxwell proposed a "time-varying electric flux" term symmetric to the changing magnetic flux in Faraday's Law to resolve this paradox. Suddenly a time-varing electric field generates a magnetic field, as well as the reverse.
Instead we postulate some pre-existing magnetic field B (Who knows where it came from? None of our business, for now.) and ask, "How does it affect a moving charged particle?" The answer (SWOP) is the Lorentz Force:
F = Q(E + v x B)
where v is the vector velocity of the particle, "x" denotes a cross product (review this!) and we have thrown in the Coulomb force due to an electrostatic field E just to make the equation complete.
Note that a bunch of charged particles flowing through a short
piece of wire (what we call a current element
I d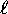 ) is interchangeable with a single
moving charge Qv. Discuss units briefly.
) is interchangeable with a single
moving charge Qv. Discuss units briefly.
Speaking of units, the Coulomb is defined as an Ampere-second, and an Ampere is defined as the current which, when flowing down each of two parallel wires exactly 1 m apart, produces a force per unit length of 2x10-7N/m between them. No kidding, that's the official definition. I'm not making this up!
Wait! It gets worse! Now try visualizing the forces between two charged particles moving at right angles to each other. What happened to Newton's Third Law?! This conundrum is only resolved by the relativistic transformations of E and B. (Stay tuned . . . . )
p = Q B r
where p is the momentum and r is the radius of the orbit. "It turns out" that this relation is relativistically correct, but you needn't concern yourself with this now.Playing with angular frequency and such reveals the nice feature that the period of the orbit is independent of the speed of the particle! This nice feature (which is not true relativistically, but only at modest speeds) is what makes cyclotrons possible. See TRIUMF.
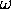 , this means
, this means 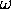 =
QB/m, a constant angular frequency (and therefore
a constant orbital period) regardless of v! Faster particles
move in proportionally larger circles so that the time for a full
orbit stays the same (as long as v << c).
This is what makes cyclotrons possible.
=
QB/m, a constant angular frequency (and therefore
a constant orbital period) regardless of v! Faster particles
move in proportionally larger circles so that the time for a full
orbit stays the same (as long as v << c).
This is what makes cyclotrons possible.
Examples: the van Allen Belt, Tokomaks and Cosmic Rays from the Universe's biggest accelerators.
Remember: the Lorentz force does no work! (It's like a really smart Physicist. :-)
 r where r is the distance from the wire. (Simple answer fron a very complicated derivation.)
r where r is the distance from the wire. (Simple answer fron a very complicated derivation.) Circular Current Loop via Biot & Savart: too hard to calculate the field anywhere except on the axis of the loop. There (by symmetry) the field can only point along the axis, in a direction given by the RHR: curl the fingers of your right hand around the loop in the direction the current flows, and your thumb will point in the direction of the resulting magnetic field. (Sort of like the loops of B around a line of I, except here B and I have traded places.) As usual, symmetry plays the crucial role: current elements on opposite sides of the loop cancel out each other's transverse field components, but the parallel (to the axis) components all add together. As for the electrostatic field due to a ring of charge, we get the same contribution to this non-canceling axial field from each element of the ring.
(Used like Gauss' Law only with a path integral.)
Long Straight Wire via Ampère's Law: It's so easy!
Any Cylindrically Symmetric current distribution gives the same result outside the conductor; inside we get an increase of B with distance from the centre, reminiscent of Gauss' Law....
Circular Current Loop via Ampère's Law: Forget it! Ampère's Law is of no use unless you can find a path around which B is constant and parallel to the path. There is no such path here.
Until about the 16th Century, science was dominated by the Aristotelian paradigm, caricatured as follows: "Get to know how things are." That is, concentrate on the phenomena; for instance, what happens when you touch a hot stove? If you asked an Aristotelian why your finger gets uncomfortably hot, the answer would be, "Because that's the way it works, stupid." We are still pretty Aristotelian in our hearts today; the textbook reflects this -- it generally delivers a concise description of "how things are" (usually as a concise formula in terms of defined quantites) and then shows how to use that principle to calculate stuff; only later (if ever) does it show why the world behaves that way. Starting nominally with Galileo, "modern scientists" began to ask questions that Aristotelians whould have considered impertinent and even arrogant, like, "Why does the heat flow the way it does?" or "How heavy is an atom?" or "Why are there only three Generations?" [The last refers to leptons and quarks, not Star Trek.]
In my opinion, PHYSICS is about those impertinent questions. It goes like this: we observe a PHEMONENON and gather empirical information about it; then we MAKE UP A THEORY for why this behaviour occurs, DERIVING it mathematically so we can check it for consistency, extend it and finally use it to PREDICT hitherto unobserved NEW phenomena as well as answering our original questions. Then we can go do EXPERIMENTS to see if the predicted phenomena do in fact occur. If not (usually), back to the drawing board. But over time, this has given us a ladder to climb....
I am going to try to follow this sequence in my lectures, so that PHYS 108 will have some of the flavour of actual science as you will experience it if you become a Scientist (not just Physicists). Some of you won't like it. Sorry. As one of the lesser philosophers of the 20th Century said, "You can't please everyone, so you have to please yourself." And speaking of songs...
(musical introduction to Thermodynamics)
I mainly want everyone to understand that the approach I am taking to introducing Thermal Physics is very unconventional, and that the glib nonsense you were probably taught in high school is not what I expect you to understand by entropy or temperature.
Every accessible fully specified state of the system is a priori equally likely.
Whoa! This has some ringers in it. We need to define (as well as we can) exactly what we mean by "accessible", "fully specified state" (or for that matter "state"), "system" and "a priori". Here we get to the details, for which I think it is appropriate to say, "You had to be there!" Some topics touched upon: Dirac notation ("|a>"), energy conservation, parking lots, counting, binomial distributions, the multiplicity function, entropy, microcanonical ensembles, maximum likelihood, extrema and derivatives, temperature and the Cuban economy.Everything is on the Thermal Physics handout (Ch. 15 of the Skeptic's Guide). I went from the beginning through the definition of (the dimensionless form of) entropy and on to the definition of inverse temperature as the criterion for the most probable configuration, i.e. thermal equilibrium. This stuff is essential, fundamental and important! I expect you to know it well enough to reproduce the derivation on an exam. (Not many things fall into this category.) Note that the derivative of entropy with respect to energy is the inverse temperature; thus when entropy is a dimensionless number, temperature is measured in energy units.
dU2 = - dU1
Does such a change lead to more overall possibilities? For a given configuration, the net multiplicity is the product of the multiplicities of the individual systems, so the net entropy is the sum of the entropies of the individual systems. If the net entropy increases when we take dU1 out of system 2 and move it into system 1, then this new configuration is more likely -- i.e. such an energy transfer will happen spontaneously. This is exactly what we mean when we say that system 2 is hotter than system 1! To turn this into a formal definition of temperature we need some mathematics..
.
.
U = (n - [N - n]) µB = (2n - N)µB
.
.
.
Mathematical derivation of the Boltzmann Distribution.
Note that the probability must be normalized.
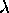 =
h/p
=
h/p
.
.
Discrete wavelengths, momenta and energies. Lowest possible energy is not zero. As the box gets smaller, the energy goes up!
Handwaving reference to black holes, relativistic kinematics, mass-energy equivalence and how the energy of confinement can get big enough to make a black hole out of even a photon if it is confined to a small enough region (Planck length).
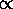
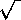 E, we expect
E, we expect
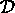 (E)
(E) 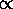 1 /
1 / 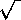 E. (Sketch.)
E. (Sketch.)
Moving to 3-D picture, there is one allowed state (mode) per unit "volume" in p-space. But if what we want is the density of states per unit magnitude of the (vector) momentum, there is a spherical shell of "radius" p and thickness dp containing a uniform "density" of allowed momenta whose magnitudes are within dp of p. This shell has a "volume" proportional to p2 and so the density of allowed states per unit magnitude of p increases as p2. This changes everything!
.
.
.
The details are on the Momentum Space handout. You may feel
this is going too far for a First Year course, and I have considerable
sympathy for that point of view. I simply wanted you to have some
idea why the Maxwellian energy and speed distributions have those
"extra" factors of 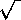 E and
v2 in them (in addition to the Boltzmann factor
itself, which makes perfect sense). The textbook (perhaps wisely)
simply gives the result, which is too Aristotelian for us, right?
E and
v2 in them (in addition to the Boltzmann factor
itself, which makes perfect sense). The textbook (perhaps wisely)
simply gives the result, which is too Aristotelian for us, right?
Rest assured that I will not ask you to reproduce any of these manipulations on any exam. At most, I will ask a short question to test whether you understand that one must account not only for the probability of a given state being occupied in thermal equilibrium (the Boltzmann factor) but also how many such states there are per unit momentum or energy (the density of states) when you want to find a distribution.
Which way is it going? To see the answer, pick a point of well defined phase on the wave (for instance, where it crosses the x axis) and then let t increase by a small amount dt. This changes the phase; what would you need to do with x to make the phase go back to its original value? If adding dx to x would compensate for the shift in t, then the wave must be moving in the positive x direction. If you must subtract dx from x to get this effect, it is moving in the negative x direction. Be sure you understand this thoroughly.
 /
/ ,
but the scalar kz is replaced by the dot product
k
,
but the scalar kz is replaced by the dot product
k r
(where r is the vector position where we want to know
the wave's amplitude). Imagine the wave "crests" as plane sheets
stretching off to infinity in both directions perpendicular to
k, marching along in the k direction
at c. Obviously the plane wave is an idealization.
We won't use this formulation explicitly very often,
but it serves to remind us that the wave has a well
defined direction of propagation, which we habitually
express in the form of rays, a picture inherited from
Newton, who insisted that light was particles following
trajectories like little billiard balls, until Huygens showed
that it was indeed waves.
(We now know they were both right!)
r
(where r is the vector position where we want to know
the wave's amplitude). Imagine the wave "crests" as plane sheets
stretching off to infinity in both directions perpendicular to
k, marching along in the k direction
at c. Obviously the plane wave is an idealization.
We won't use this formulation explicitly very often,
but it serves to remind us that the wave has a well
defined direction of propagation, which we habitually
express in the form of rays, a picture inherited from
Newton, who insisted that light was particles following
trajectories like little billiard balls, until Huygens showed
that it was indeed waves.
(We now know they were both right!)
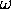 = c k, then
vg =
d
= c k, then
vg =
d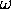 /dk = c =
/dk = c =
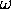 /k = vp
/k = vp
But there are lots of other wave equations (a good example
being the Schroedinger Equation for "matter waves" which you will
encounter next year if you take Physics 200) which do not
have this simple linear relationship between the frequency and the
wavelength. We will not dwell on this in P108, but you should be
aware that actual information (or matter itself, in the
case of matter waves) moves at the group velocity
vg =
d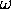 /dk,
not at the phase velocity vp =
/dk,
not at the phase velocity vp =
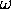 /k.
/k.
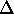
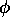 = 2
= 2 )
at reflection from a denser medium
with a larger index of refraction
(like for a rope attached to the wall);
phase does not reverse at reflection from a less dense
medium with a smaller index of refraction (like for a rope with a
dangling end).
)
at reflection from a denser medium
with a larger index of refraction
(like for a rope attached to the wall);
phase does not reverse at reflection from a less dense
medium with a smaller index of refraction (like for a rope with a
dangling end).
Refraction: "slow light" -- index of refraction n = cvacuum/c'medium (always 1 or greater).
Snell's Law: n sin 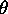 = n' sin
= n' sin 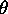 '.
'.
Total Internal Reflection (Ltd.)
"Effective path length"
Disturbances of a linear medium just add together. Thus if one wave is consistently "up" when the other is "down" (i.e. they are "180o out of phase") then the resultant amplitude at that position is zero. This is called "destructive interference". If they are both "up" (or "down") at the same time in the same place, that's "constructive interference".
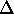
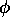 = 2
= 2 (
(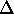
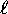 /
/ )
due to the path length difference
)
due to the path length difference
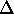
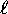 and you have the net phase difference between the two reflected waves.
When this is an integer multiple of
2
and you have the net phase difference between the two reflected waves.
When this is an integer multiple of
2 you have constructive
interference. When it is an odd multiple of
you have constructive
interference. When it is an odd multiple of
 , you have destructive
interference. That's really the whole story.
, you have destructive
interference. That's really the whole story.
Examples: the "quarter wave plate" and the soap film. Oil on water and the fish poem.
Vector fields and visualization.
Simple problems with point charges. Superposition of electric fields from different sources - just add 'em up (vectorially)!
Not so simple problems: continuous charge distributions.
Example: the electric field on axis due to a ring of charge can only be calculated by "brute force" integrating Coulomb's Law. Fortunately it is quite easy, as long as we stay on the axis where transverse components cancel by symmetry.
Slightly harder: the electric field on axis due to a disc of charge is the sum of the fields from all the little rings that make up the disc.
Always check that the result you calculate behaves as expected (namely, Coulomb's Law) as you get so far away from the charged object that it looks like a point charge.
Possible motions of a rigid body:
Inertial factors: we are used to m being a fixed, scalar property of a particle, determining both how much F it takes to produce any a and how much p we get for a given v. In the same way, there is a measure of rotational inertia called the moment of inertia IA about axis A that tells us how much torque it takes to produce a given angular acceleration and how much angular momentum we get for a given angular velocity.
Show for an arbitrary axis through an arbitrary rigid body that the moment of inertia about that axis is the sum (integral) of the square of the perpendicular distance from the axis times the element of mass at that distance.
Thus the moment of inertia of a hoop of mass M and radius R about a perpendicular axis through its centre is ICM = MR2. The same goes for a cylindrical shell. More examples on Friday.
IA = ICM + M h2.
Iz = Ix + Iy.
ICM = (1/12)M L2.
Iz = (1/12)M (Lx2 + Ly2).
ICM = (1/2)M R2.
ICM = (2/3)M R2.
ICM = (2/5)M R2.
Each of these takes a little while to calculate, and the only difference between them is the numerical factor out in front of the M R2 or M L2 or whatever.Although you can do the calculation yourself using only simple integrations and the two Theorems described above, this is one of those few cases where it is a good idea to just memorize the numerical factors that go with the different common shapes, to save yourself time and energy on homework and exams.
K = (1/2)M V2 +
(1/2) ICM 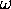 2
2
(Several theories proposed; vote taken on which was wrong.)
Explanation: In general, the angular motion is independent of the translational motion. But in the case of rolling without slipping, the position on the surface is locked to the angle through which the wheel has turned, and so likewise the speed parallel to the plane and the angular velocity of rolling:
v = R
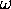 .
.
Adding Resistances: in series (just add 'em up!) and in parallel (add inverses to get equivalent inverse).
Kirchhoff's Rules:
Now you understand both C and R. Let's put them together.
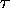 = RC.
= RC. Now do it mathematically: solve the differential equation for Q(t).
Drift velocity vd = acceleration (eE/m) 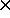 mean time between scattering collisions
mean time between scattering collisions 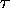 .
.
Problem: how can 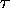 be independent of the "steepness of the slope"? Short excursion into Quantum Mechanics and Fermi-Dirac statistics: electrons are fermions (half-integer spin) so no two electrons can be in the same state. Thus the lowest energy states are all full and the last electrons to go into a metal occupy states with huge kinetic energies (for an electron) comparable to 1 eV or 10,000 K. Only the electrons at this "Fermi level" can change their states, so only they count in conduction. So our ideal skiers actually have rocket-propelled skis and are randomly slamming into trees (and each other) at orbital velocities (we will neglect the problems of air friction); the tiny accumulated drift downhill is imperceptible but it accounts for all conduction.
be independent of the "steepness of the slope"? Short excursion into Quantum Mechanics and Fermi-Dirac statistics: electrons are fermions (half-integer spin) so no two electrons can be in the same state. Thus the lowest energy states are all full and the last electrons to go into a metal occupy states with huge kinetic energies (for an electron) comparable to 1 eV or 10,000 K. Only the electrons at this "Fermi level" can change their states, so only they count in conduction. So our ideal skiers actually have rocket-propelled skis and are randomly slamming into trees (and each other) at orbital velocities (we will neglect the problems of air friction); the tiny accumulated drift downhill is imperceptible but it accounts for all conduction.
J = "flux" of charge = current per unit perpendicular area (show a "slab" of drifting charge) so J = n e vd, where n is number of charge carriers per unit volume. (For Cu, n is about 1029 m-3.)
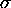 E, defining the conductivity
E, defining the conductivity 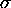 = n e2
= n e2 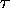 /m, measured in Siemens per metre (S/m) if you like SI units (1 S = 1 A/V). I don't.
/m, measured in Siemens per metre (S/m) if you like SI units (1 S = 1 A/V). I don't. For Cu, 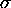 is around 108 S/m. Putting this together with n, e and me = 9 x 10-31 kg, we get
is around 108 S/m. Putting this together with n, e and me = 9 x 10-31 kg, we get 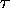 ~ 10-13 s. At vF ~ 106 m/s this implies a mean free path
~ 10-13 s. At vF ~ 106 m/s this implies a mean free path 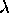 ~ 10-7 m. Compare lattice spacing ~ 10-10 m. The drift velocity vd is only ~ 10-3 m/s.
~ 10-7 m. Compare lattice spacing ~ 10-10 m. The drift velocity vd is only ~ 10-3 m/s.
In semiconductors, n is a factor of 10-7 smaller and vd is a factor of 107 larger, almost as big as vF! So in some very pure semiconductors transport is almost "ballistic", especially when the size of the device is less than 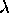 .
.
Briefly discuss superconductors.
The inverse of the conductivity is the resistivity 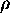 , measured in Ohm-meters. (1 Ohm = 1 V/A).
, measured in Ohm-meters. (1 Ohm = 1 V/A).
Use a cartoon of a cylindrical resistor of length L and cross-sectional area A to remind how this works, giving R = 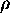 L/A and the familiar V = I R.
L/A and the familiar V = I R.
Instead we postulate some pre-existing magnetic field B (Who knows where it came from? None of our business, for now.) and ask, "How does it affect a moving charged particle?" The answer (SWOP) is the Lorentz Force:
F = Q(E + v x B)
where v is the vector velocity of the particle, "x" denotes a cross product (review this!) and we have thrown in the Coulomb force due to an electrostatic field E just to make the equation complete.Note that a bunch of charged particles flowing through a short piece of wire (what we call a current element I d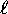 ) is interchangeable with a single moving charge Qv.
) is interchangeable with a single moving charge Qv.
Wait! It gets worse! Now try visualizing the forces between two charged particles moving at right angles to each other. What happened to Newton's Third Law?! This conundrum is only resolved by the relativistic transformations of E and B. (Stay tuned . . . . )
 =
= a sin  1 =
1 =  .
.
 equal to zero (condition for an extremum), giving
equal to zero (condition for an extremum), giving
The narrower the slit, the wider the diffraction pattern. Picture a circular aperture as a square aperture with the "corners chopped off": on average, it is narrower than the original square whose side was equal to the circle's diameter. Thus you would expect it to produce a wider diffraction pattern. It does! The numerical difference is a factor of 1.22:
a sin  1 = 1.22
1 = 1.22  .
.
Dm = d m/d
m/d = m/d cos
= m/d cos  m .
m .
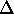
 ) can two colours be and still be resolved by the grating?
) can two colours be and still be resolved by the grating? Well, the two lines will just be resolved when the mth order principal maximum of one falls on top of the first minimum beyond the mth order principal maximum of the other.
By requiring the path length difference between adjacent slits to differ (for the two colours) by  /N (where N is the number of slits) we ensure that the phasor diagram for the second colour will just close (giving a minimum) when that of the first colour is a principal maximum. This gives a resolving power
/N (where N is the number of slits) we ensure that the phasor diagram for the second colour will just close (giving a minimum) when that of the first colour is a principal maximum. This gives a resolving power
Rm =  /
/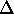
 = m N .
= m N .
Vector fields and visualization.
Simple problems with point charges. Superposition of electric fields from different sources - just add 'em up (vectorially)!
Not so simple problems: continuous charge distributions.
Example: the electric field on axis due to a ring of charge can only be calculated by "brute force" integrating Coulomb's Law. Fortunately it is quite easy, as long as we stay on the axis where transverse components cancel by symmetry.
Slightly harder: the electric field on axis due to a disc of charge is the sum of the fields from all the little rings that make up the disc.
Always check that the result you calculate behaves as expected (namely, Coulomb's Law) as you get so far away from the charged object that it looks like a point charge.
PDF or printer-friendly gzipped PostScript files
Then move on to a hard (but not impossible) problem: the electric field due to a Finite Rod of Charge. See also the usual PDF and printer-friendly gzipped PostScript files.
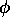 ["phi"] (chosen in class) because HTML still has no Greek letters except "µ". I can get away with this on the computer because the math symbol V (for potential) is italicized while the abbreviation "V" (for "Volts") is not; so I can write "V = 4 V" without ambiguity.
["phi"] (chosen in class) because HTML still has no Greek letters except "µ". I can get away with this on the computer because the math symbol V (for potential) is italicized while the abbreviation "V" (for "Volts") is not; so I can write "V = 4 V" without ambiguity. In principle, it's easier to find E from V (using E = - 
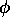 ) than vice versa, because it's a lot easier to integrate up a scalar function than a vector one! (And derivatives are easy, right?) However, in practice (at the level of P108) we are not going to be evaluating arbitrary, asymmetric charge distributions, but only the simple symmetric shapes and combinations thereof (using the principle of additive superposition). In these cases Gauss' Law allows us to find E easily and find V by simple integrations; so that's mostly what we do.
) than vice versa, because it's a lot easier to integrate up a scalar function than a vector one! (And derivatives are easy, right?) However, in practice (at the level of P108) we are not going to be evaluating arbitrary, asymmetric charge distributions, but only the simple symmetric shapes and combinations thereof (using the principle of additive superposition). In these cases Gauss' Law allows us to find E easily and find V by simple integrations; so that's mostly what we do.
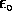 by
by  =
= 
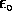 (where
(where  is the dielectric constant, a pure number always
is the dielectric constant, a pure number always 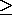 1) and everything takes care of itself. Thus C always gets bigger (by a factor of
1) and everything takes care of itself. Thus C always gets bigger (by a factor of  ) when there is a dielectric in between the plates. [Explain.]
) when there is a dielectric in between the plates. [Explain.] For isotropic, cylindrical and planar geometries, show how potential is calculated from the electric field and how capacitance is in turn calculated from that. See PDF or printer-friendly gzipped PostScript files.
An array of capacitors in parallel has an equivalent capacitance equal to the sum of their separate capacitances. [Explain.]
An array of capacitors in series has an equivalent inverse capacitance equal to the sum of their separate inverse capacitances. [Explain.]
The energy required to put a charge Q on a capacitor C is not just VQ! The first bit of charge goes on at zero voltage (no work) and the voltage (work per unit charge added) increases linearly with Q as the charge piles up: V = (1/C) Q. Thus dU = (1/C) Q dQ. Integrating yields U = (1/2C) Q2 or U = (1/2)C V2.
For a parallel plate capacitor, V = E d and C = 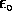 A / d. Thus U = (1/2)
A / d. Thus U = (1/2)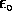 AE2 d. But A d is the volume of the interior of the capacitor (the only place where the electric field is nonzero). Thus if u is defined to be the energy density per unit volume, then we have u = (1/2)
AE2 d. But A d is the volume of the interior of the capacitor (the only place where the electric field is nonzero). Thus if u is defined to be the energy density per unit volume, then we have u = (1/2)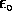 E2. "It turns out" that this prescription is completely general! Wherever there is an electric field, energy is stored at a density u given by the formula above.
E2. "It turns out" that this prescription is completely general! Wherever there is an electric field, energy is stored at a density u given by the formula above.
It is now getting really tempting to think of E as something "real", not just a mathematical abstraction.
A D = Qenclosed
where for additional simplicity we have defined D =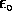 E.
E. If time permits, begin discussion of conductors.
Standing Waves: The most familiar example to players of stringed instruments is probably the case of two waves of equal amplitude, wavelength and frequency propagating in opposite directions (which can be represented mathematically by giving either k or 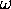 [but not both] opposite signs for the two waves). In this case we get a wave which no longer "travels" but simply "oscillates in place" with nodes where no motion ever occurs. The "particle in a box" example shares with the closed organ pipe and the guitar string the feature that there must be nodes at the ends of the box/pipe/string, a feature that forces quantization of modes even for classical waves.
[but not both] opposite signs for the two waves). In this case we get a wave which no longer "travels" but simply "oscillates in place" with nodes where no motion ever occurs. The "particle in a box" example shares with the closed organ pipe and the guitar string the feature that there must be nodes at the ends of the box/pipe/string, a feature that forces quantization of modes even for classical waves.
Beats - Interference in Time: If two waves pass the same location in space (your ear, for instance) with slightly different frequencies then they drift slowly into and out of phase, resulting in a sound of the average frequency whose average amplitude (or its square, the intensity) oscillates at a frequency equal to the difference between the two original frequencies. This is a handy method for tuning guitar strings: as their frequencies of vibration get closer together, the beat frequency gets slower, until it disappears entirely when they are exactly in tune.
Interference in Space: This applies only for waves with the same frequency. Consider two waves of equal amplitude: If one wave is consistently "up" when the other is "down" (i.e. they are "180o out of phase") then the resultant amplitude at that position is zero. This is called "destructive interference". If they are both "up" (or "down") at the same time in the same place, that's "constructive interference".
Thin Films: Assuming normal incidence, add together the "rays" reflected from both surfaces of the film. Remember the phase change at any reflections from denser media. Then add in the phase difference 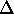
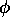 = 2
= 2 (
(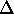
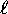 /
/ ) due to the path length difference
) due to the path length difference 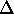
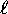 and you have the net phase difference between the two reflected waves. When this is an integer multiple of 2
and you have the net phase difference between the two reflected waves. When this is an integer multiple of 2 you have constructive interference. When it is an odd multiple of
you have constructive interference. When it is an odd multiple of  , you have destructive interference. That's really the whole story.
, you have destructive interference. That's really the whole story.
Examples: the "quarter wave plate" and the soap film. Oil on water and the fish poem.
 ) to defined the adjacent "wave front". Naturally we make no attempt to draw 3D spherical waves on a flat page; all the 2D pictures are meant only as "conceptual shorthand". This will be even more abstract as we start drawing "phasor" diagrams.
) to defined the adjacent "wave front". Naturally we make no attempt to draw 3D spherical waves on a flat page; all the 2D pictures are meant only as "conceptual shorthand". This will be even more abstract as we start drawing "phasor" diagrams. Be sure to review your trigonometry - we'll be using it!
The "near field" intensity pattern (where "rays" from the two sources, meeting at a common point, are not even approximately parallel) is difficult to calculate, though it is easy enough to describe how the calculation could be done. We will stay away from this region - far away, so that all the interfering rays may be considered parallel. Then it gets easy!
Simplified sketch assuming incident waves hitting the barrier in phase (i.e. normal incidence) shows an obvious path length difference of 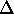
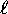 = d sin
= d sin  between the waves heading out from the two slits at that angle. If this path length difference is an integer multiple of the wavelength
between the waves heading out from the two slits at that angle. If this path length difference is an integer multiple of the wavelength  we get constructive interference. This defines the nth Principal Maximum (PM):
we get constructive interference. This defines the nth Principal Maximum (PM):
d sin  n = n
n = n 
 n from the normal direction. We always define x = 0 to be the position of the central maximum (CM) - i.e.
n from the normal direction. We always define x = 0 to be the position of the central maximum (CM) - i.e.  = 0. If the distance L from the slits to the screen is >> d (the distance between the slits), as it almost always is, then we can use the small angle approximations sin
= 0. If the distance L from the slits to the screen is >> d (the distance between the slits), as it almost always is, then we can use the small angle approximations sin 
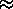 tan
tan 
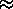
 so that
so that  n
n 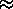 n
n  /d and xn = L tan
/d and xn = L tan  n
n 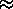 L
L  n giving xn
n giving xn 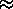 n L
n L  /d.
/d. Be sure you can do calculations like these yourself. Such problems are almost always on the final exam.
Time permitting, I will start on Multiple Slit Interference. The handout covers this in detail; if I don't cover it today, be sure to study the handout over the weekend!
In this abstract world each wave is seen as an amplitude Ai pointing away from some origin at a phase angle 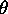 i in "phase space" - a phasor. All the phasors representing different wave amplitudes are "precessing" about the origin at a common angular frequency
i in "phase space" - a phasor. All the phasors representing different wave amplitudes are "precessing" about the origin at a common angular frequency 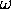 (the actual frequency of the waves) but their phase differences do not change with time. Thus we can pick one wave arbitrarily to have zero phase and "freeze frame" to show the angular orientations (and lengths) of all the others relative to it.
(the actual frequency of the waves) but their phase differences do not change with time. Thus we can pick one wave arbitrarily to have zero phase and "freeze frame" to show the angular orientations (and lengths) of all the others relative to it.
Phasors are vectors (albeit in a weird space) and so if they are to be added linearly we can construct a diagram for the resultant by drawing all the amplitudes "tip-to-tail" as for any vector addition. If there are any configurations that "close the polygon" (i.e. bring the tip of the last phasor right back to the tail of the first) then the net amplitude is zero and we have perfect destructive interference!
For an idealized case of N equal-amplitude waves out of phase with their neighbours by an angle 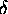 we will get a minimum when N
we will get a minimum when N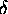 = n(2
= n(2 ), satisfying the above criterion. This is the condition for the nth minumum of the N-slit interference pattern; we usually only care about the first such minimum, which occurs where N
), satisfying the above criterion. This is the condition for the nth minumum of the N-slit interference pattern; we usually only care about the first such minimum, which occurs where N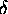 = 2
= 2 .
.
To see where in real space that first minimum occurs, we have to go back to the origin of the phase differences due to path length differences: 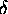 /2
/2 =
= 
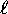 /
/ = d sin
= d sin  /
/ , giving
, giving
d sin  first min. =
first min. =  /N .
/N .
Maxwell proposed a "time-varying electric flux" term symmetric to the changing magnetic flux in Faraday's Law to resolve this paradox. Suddenly a time-varing electric field generates a magnetic field, as well as the reverse.
So now we have Gauss' Law in two forms (integral over a closed surface vs. differential at any point in space) for E (or, better yet, for D = 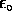 E) and for B (where it may seem trivial to express the fact that there don't seem to be any magnetic "charges" [monopoles] but in fact this is quite useful).
E) and for B (where it may seem trivial to express the fact that there don't seem to be any magnetic "charges" [monopoles] but in fact this is quite useful).
We have Faraday's Law also in two forms; we will only be using the integral form in this course, but you should be able to recognize the differential form.
And we have Maxwell's corrected version of Ampère's Law which again we will be using here only in the integral form but you should be able to recognize in either form.
These 4 Laws constitute Maxwell's Equations, which changed the world. To complete "everything you need to know about electromagnetism on one page" you should include the Lorentz Force Law (including the electric force) and the Equation of Continuity (which simply expresses the conservation of charge). That's it. Real simple "cheat sheet", eh?
From Ampère's Law applied to a specific geometry we have the first mixed time- and space-derivative equation. I will derive this today and then move on to the next equation which comes from Faraday's Law.
To get the definition of a Tesla [T] we have to wait until the next Chapter on where magnetic fields come from, i.e. the Law of Biot & Savart.
p = Q B r
where p is the momentum and r is the radius of the orbit. "It turns out" that this relation is relativistically correct, but you needn't concern yourself with this now. Since v = r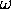 , this means
, this means 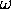 = QB/m, a constant angular frequency (and therefore a constant orbital period) regardless of v!
(This, unfortunately, is not relativistically correct.) Faster particles move in proportionally larger circles so that the time for a full orbit stays the same (as long as v << c). This is what makes cyclotrons possible. At TRIUMF, since v ~ c, we have to resort to an ingenious trick to compensate for relativity.
= QB/m, a constant angular frequency (and therefore a constant orbital period) regardless of v!
(This, unfortunately, is not relativistically correct.) Faster particles move in proportionally larger circles so that the time for a full orbit stays the same (as long as v << c). This is what makes cyclotrons possible. At TRIUMF, since v ~ c, we have to resort to an ingenious trick to compensate for relativity. (Used like Gauss' Law only with a path integral.)
Long Straight Wire via Ampère's Law: It's so easy!
Any Cylindrically Symmetric current distribution gives the same result outside the conductor; inside we get an increase of B with distance from the centre, reminiscent of Gauss' Law....
Circular Current Loop via Ampère's Law: Forget it! Ampère's Law is of no use unless you can find a path around which B is constant and parallel to the path. There is no such path here.
By the same logic as for electric dipole moments in electric fields, the potential energy of the magnetic dipole in the magnetic field is minus the scalar ("dot") product of µ with B. This may be familiar from Thermal Physics.
For details see PDF or printer-friendly gzipped PostScript files.
Much of the lecture was presented using Open Office, a free, Open Source replacement for Micro$oft Office. You are welcome to download the PDF file if you like; I will make the Open Office or PPT file available on request.
We have to remember that the total energy U is conserved. Thus dU1 = - dU2.
A maximum of the total entropy occurs where its rate of change with respect to U1 is zero.
Working this out in detail gives a definition of temperature.
We use this definition to examine the thermal behaviour of an unusual system: N spin 1/2 electrons in an applied magnetic field B. The exotic features of this system are due to its unusual feature of having a limit to the amount of energy U it can "hold". We correctly expect that the number of ways it can have that maximum energy (where all the spins are "up") is 1, so at the maximum U the entropy is zero; since it is nonzero at lower U, it must be decreasing with U for energies approaching the maximum. Thus the slope of entropy vs. energy starts positive, goes down through zero and then becomes negative. Since this is the inverse temperature, the temperature itself starts low, goes to infinity, flips to negative infinity and finally approaches zero from the negative side. What does this mean?!
Negative temperatures exist. It is easy to make them in the lab. They are hotter than positive temperatures (even hotter than infinite positive temperature!); the hottest temperature of all is "approaching zero from below". This weirdness is the result of our insistence that "hot" must mean "high temperature", requiring the definition of temperature as the inverse of the slope of entropy vs. energy. Live with it.
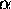 " it is in. We are allowed (indeed, we are encouraged) to narrow our focus to just one degree of freedom of one particle (or whatever), such as the "system" consisting of the orientation of the spin of a single electron.
" it is in. We are allowed (indeed, we are encouraged) to narrow our focus to just one degree of freedom of one particle (or whatever), such as the "system" consisting of the orientation of the spin of a single electron.
The energy contained in this small system S in state "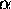 " is called
" is called 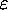
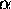 .
We imagine that this energy was removed from the reservoir R, to make its energy UR = U -
.
We imagine that this energy was removed from the reservoir R, to make its energy UR = U - 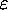
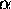 , where U is the total energy of the combined systems (and was the energy of R before we tapped some off into S).
, where U is the total energy of the combined systems (and was the energy of R before we tapped some off into S).
This process changes the entropy of R by an amount . . . well, this is more easily displayed in a PDF file or (if you want a more printer-friendly format) a gzipped PostScript file.
PRESSURE: A single particle bouncing around in a box with perfectly elastic specular collisions causes an average force on the walls of the box.
IDEAL GAS:
As usual, a more complete graphical summary is available in PDF or gzipped PostScript format.
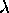 = h/p
= h/p
.
.
Discrete wavelengths, momenta and energies. Lowest possible energy is not zero. As the box gets smaller, the energy goes up!
Handwaving reference to black holes, relativistic kinematics, mass-energy equivalence and how the energy of confinement can get big enough to make a black hole out of even a photon if it is confined to a small enough region (Planck length).
For more details see PDF or print-friendly gzipped PostScript files.
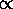
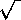 E, we expect
E, we expect
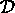 (E)
(E) 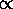 1 /
1 / 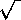 E. (Sketch.)
E. (Sketch.)
Moving to 3-D picture, there is one allowed state (mode) per unit "volume" in p-space. But if what we want is the density of states per unit magnitude of the (vector) momentum, there is a spherical shell of "radius" p and thickness dp containing a uniform "density" of allowed momenta whose magnitudes are within dp of p. This shell has a "volume" proportional to p2 and so the density of allowed states per unit magnitude of p increases as p2. This changes everything!
.
.
.
The details are on the Momentum Space handout and in the PDF and printer-friendly gzipped PostScript files from the graphical presentation in class.
You may feel
this is going too far for a First Year course, and I have considerable
sympathy for that point of view. I simply wanted you to have some
idea why the Maxwellian energy and speed distributions have those
"extra" factors of 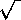 E and
v2 in them (in addition to the Boltzmann factor
itself, which makes perfect sense). The textbook (perhaps wisely)
simply gives the result, which is too Aristotelian for us, right?
E and
v2 in them (in addition to the Boltzmann factor
itself, which makes perfect sense). The textbook (perhaps wisely)
simply gives the result, which is too Aristotelian for us, right?
Rest assured that I will not ask you to reproduce any of these manipulations on any exam. At most, I will ask a short question to test whether you understand that one must account not only for the probability of a given state being occupied in thermal equilibrium (the Boltzmann factor) but also how many such states there are per unit momentum or energy (the density of states) when you want to find a distribution.
 /
/ , but the scalar kz is replaced by the dot product k
, but the scalar kz is replaced by the dot product k r (where r is the vector position where we want to know the wave's amplitude). Imagine the wave "crests" as plane sheets stretching off to infinity in both directions perpendicular to k, marching along in the k direction at c. Obviously the plane wave is an idealization. We won't use this formulation explicitly very often, but it serves to remind us that the wave has a well defined direction of propagation, which we habitually express in the form of rays, a picture inherited from Newton, who insisted that light was particles following trajectories like little billiard balls, until Huygens showed that it was indeed waves. (We now know they were both right!)
r (where r is the vector position where we want to know the wave's amplitude). Imagine the wave "crests" as plane sheets stretching off to infinity in both directions perpendicular to k, marching along in the k direction at c. Obviously the plane wave is an idealization. We won't use this formulation explicitly very often, but it serves to remind us that the wave has a well defined direction of propagation, which we habitually express in the form of rays, a picture inherited from Newton, who insisted that light was particles following trajectories like little billiard balls, until Huygens showed that it was indeed waves. (We now know they were both right!) Continue with a brief review of 3-dimensional vectors. Make sure you can do all the operations "in your sleep", both analytically (using algebra and the left hemisphere of your brain, which is reputed to handle abstract symbolic logic) and graphically (using various physical analogues and the right hemisphere of your brain, which is said to govern intuition and spatial vision). Whatever tricks you use to remember the "right hand rule" convention for "cross products", be sure they are well practiced; we'll be using them a lot when we get to Magnetism!
Then on to our first topic in Electricity & Magnetism (E&M): the Coulomb force between electric charges.
A comparison of the gravitational force between masses with the electrostatic force between charges shows just two differences:
As usual, details are available in either PDF or printer-friendly gzipped PostScript format. First I need to know a bit about you and your expectations/preferences. Who are you? How much do you already know about Physics? How seriously do you take Poetry? What did you think this course was going to be about? What would you like this course to be about? Do you expect to do any homework? Reading? Do you mind doing some things on the computer? Do you have access to the Web? (If the consensus is negative on the last question, then you are probably not reading this; so you can tell I am hoping to be able to use Web tools with the course.) While I am a tireless advocate for Poetry, I have no credentials as a Poet, and there are bound to be at least some of you who do; so I will never be tempted to speak with Authority about that discipline - all my pronunciamentos will be understood to represent only my own opinion, and counteropinions will be welcome. Just don't go all ad hominum on me, OK? I do have some Physics credentials, however undeserved, and I have a few favourite topics I'd love to weave into this short week if I can. I'll list a few of them below and ask you to give me some feedback on which you'd like me to concentrate upon. There's more, of course, but we'll build on your preferences and follow the discussion where it leads.
"What Does It All Mean?"
Course
"Elementary Particles"
Topic
Found 1 Lectures on Fri 31 Jan 2025.
"Small Stuff"
by Jess H. Brewer
on 2005-06-17:
"Introduction"
Topic
Found 2 Lectures on Fri 31 Jan 2025.
"Introduction"
by Jess H. Brewer
on 2005-06-10:
"Emergence"
by Jess H. Brewer
on 2005-06-13: Tacit Knowledge
Before we can "grow new language" we need to have a vocabulary of familiar "old" words to juxtapose in unfamiliar ways. In Physics everything starts from Classical (Newtonian) Mechanics, which in turn starts from the familiar equation F = m a, where F is the net force exerted on some body, m is its mass and a is the resulting acceleration. This isn't actually the way Newton expressed his "First Law", but it will do. Most people are fairly familiar with this Law by the time they reach University, so it serves as an example of what Michael Polanyi would call "Tacit Knowledge" - things we know so well they are "obvious" and/or "Common Sense". Emergence
In the The Skeptic's Guide chapter on Mechanics I show how F = m a can be "morphed" by mathematical identities into principles that appear to be different, like Conservation of Impulse and Momentum, Conservation of Work and Energy or Conservation of Torque and Angular Momentum. There is really nothing new in these principles, but we gain insight into the qualitative behaviour of Mechanics from the exercise. Thus new Common Sense emerges from the original language by a process analogous to metaphor in Poetry.
In the same way, bizarre phenomena like superconductivity emerge in the behaviour of many crystals, even though every detail of the interactions between their components is completely understood. When the familiar is combined in new ways, the unfamiliar emerges, and it is often very unfamiliar. This seems to be characteristic not only of what Physicists do, but also of how Nature behaves!
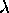 related by
related by 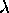 = h/p and p = h/
= h/p and p = h/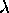
Whatever we might "mean" by this, it has some dramatic consequences: imagine that we have confined a single particle to a one-dimensional "box". Examples would be a bead on a frictionless wire, or an electron confined to a long carbon nanotube (or a DNA molecule); both of the latter two examples are currently being studied very enthusiastically as candidates for nanotechnology components, so they are not the usual frivolous Physics idealizations!
If the particle is really like a wave, then the wave must have nodes at the ends of the box, just like the standing waves on a guitar string or the sound waves on a closed organ pipe. This means there are discrete "allowed modes" with integer multiples of 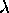 /2 fitting into the length L of the "box". Not all wavelengths are allowed in the box, only those satisfying this criterion; therefore, not all momenta are allowed for the particle bouncing back and forth between the ends of the box, only those corresponding to the discrete ("quantized") allowed wavelengths.
/2 fitting into the length L of the "box". Not all wavelengths are allowed in the box, only those satisfying this criterion; therefore, not all momenta are allowed for the particle bouncing back and forth between the ends of the box, only those corresponding to the discrete ("quantized") allowed wavelengths.
Since the kinetic energy of the particle increases as its momentum increases, the lowest allowed energy state is the one whose wavelength is twice the length of the box, and if the box shrinks, this "ground state" energy increases. Moreover, since the particle is bouncing back and forth off the ends of the box (like a ping pong ball between the table top and a descending paddle), the average force exerted by the particle on the walls of its confinement increases as the walls close in.
Is this not a lovely metaphor? Like most people, every particle (because it is also a wave) cries, "Don't fence me in!" and will resist confinement with ever increasing vigour as the walls close in.
This resistance eventually goes beyond mere force. If you will allow me to state without adequate explanation that Einstein's famous equation "E = m c2" means not only that any mass m represents a large amount of energy E, but also that energy stored up in a small region has an effective mass, with all the concomitant effects such as gravitational attraction for other masses, then you will see that as the confined particle's energy increases (due to tighter and tighter confinement) it begins to have a gravitational field. And if its energy increases enough it will act as a "black hole" for other objects within L of the box - including the walls of the box! At this length scale (called the Planck length) all bets are off - we do not understand physics at this level of "quantum gravity", although armies of Physicists are now working on it.
So the humblest particle, even the photon (which has no rest mass), will eventually dismantle its jail even if it has to deconstruct the very Laws of Physics to do so. A fine example for us all, I think, and an apt mascot for Amnesty International!
Towards the end I did manage to get started talking about the implications of de Broglie's hypothesis that all particles are also waves, and vice versa, with their momentum p and their wavelength 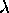 related by
related by
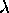 = h/p and p = h/
= h/p and p = h/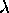
This also took up too much time, but who's counting? :-)
On to stress as force per unit area: if the force is normal to the area element, we have pressure, but if it is parallel to the surface, we have (two components of) shear. This applies to all three choices of surface normal and to all three force directions for each, giving a Stress Tensor Tij = dFi/daj, a 3x3 matrix with only 6 independent elements, since it must be symmetric (Tij = Tji).
Challenge Question: Why must the stress tensor be symmetric?
Getting back (finally) to E&M, we had derived an expression for the time rate of change of mechanical momentum density due to electromagnetic fields that had a term that reduces to [minus the time rate of change of the Poynting vector over c2] (i.e. minus the time rate of change of electromagnetic momentum density, which we can take over to the other side of the equation to add all the momentum density together) plus a term in E and its spatial derivatives, a term in B and its spatial derivatives, and minus the gradient of the electromagnetic energy density. These three terms are what Griffiths calls the "ugly" part of f, so I'll designate it as fugly.
If only fugly were the divergence of something "??", we could convert the volume integral of fugly into a surface integral of "??". The problem is, usually a divergence is a scalar, but now it has to be a vector. So "??" isn't a vector; it has to be a tensor. This is clumsy to represent vectorially, but easy in component notation: we want to find a Tij such that fjugly = di Tij. Can we arrange this? Griffiths (and all other textbooks that I have seen) simply offer the answer; I'd prefer to show how to deduce the desired form of Tij, but I've run out of time today.
Stay tuned . . .
Tij = 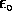 (EiEj -
(EiEj - 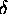 ijE2/2) + (BiBj -
ijE2/2) + (BiBj - 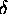 ijB2/2)/
ijB2/2)/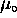 .
.
I advise everyone to study Example 8.2 (pp. 353-355) carefully! There is real magic in Tij, because it "knows" what is going on inside a region just from its integral over any surface containing that region. Note in particular that you can choose different surfaces (as long as they contain the same region and no others with different charges) and it will give the same answer for the net EM force on the charges in that region.
The disadvantage of using Tij is that it is intrinsically and irreducibly (I think) cartesian. Any curvilinear coordinates have to be expressed in terms of (x, y, z) consistent with Tij.
That completes our reformulation of the sacred principle of momentum conservation to take into account the effects of EM fields and the momentum they carry. What about the other sacred conservation principle?
Angular Momentum Conservation: If S/c2 is the electromagnetic momentum density per unit volume at some point in space, then the electromagnetic angular momentum density per unit volume at the same point, relative to some origin, is r x S/c2. I use this to work out a slightly altered version of Example 8.4 on pp. 359-361 and explain why Feynman's "disc paradox" isn't. (A paradox, that is.)
I also encourage everyone to tackle Problem 8.12 "just for fun", so see for themselves exactly why people claim that the existence of a single magnetic monopole implies charge quantization. (Conundrum du jour: what if there are two magnetic monopoles of different sizes?)
eiθ = cos θ + i sin θ
This allows us to write plane waves asψ = ψ0 ei(k•x - ωt)
for which the taking of derivatives becomes trivial:∂ψ/∂t = -iω ψ and ∇ψ = ik ψ
which we can extend to vector EM waves by substituting E (or B) for ψ, giving∂E/∂t = -iω E , ∇ • E = ik • E and ∇ x E = ik x E
Note however, that only the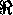 part is real! Once all the derivatives have been taken, before you calculate anything measurable, throw away the
part is real! Once all the derivatives have been taken, before you calculate anything measurable, throw away the 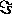 part. (This will be especially important when we start discussing energy density and momentum transport!)
part. (This will be especially important when we start discussing energy density and momentum transport!) Conundrum du Jour: What if Ï â‰ 0? Is E still always ⊥ k?
This still would allow arbitrary relative magnitudes and orientations (in the plane ⊥ k) of E and B, but Faraday's law says ∇ x E = - ∂B/∂t or ik x E = iωB so if we divide through by k=|ik| and note that ω/k = c, we getn x E = cB
where n = k/k is a unit vector in the direction of propagation. This fixes not only the relative directions of n, E and B (all perpendicular) but also the relative magnitudes of E and B: E = c B.Next topic (after the Midterm): energy and momentum transport.
Energy Density: uEM = (εE2 + B2/μ)/2. Again plugging in the above relationships between the two fields gives uEM = εE2 = B2/μ (either will serve). Putting this together with the Poynting vector gives S = v uEM, as expected.
Time-Averaged Energy Transport: Since both E and B are oscillatory, the time average of the square of either one is half its maximum amplitude ( Momentum Density: Recall that S/v2 is the momentum per unit volume transported by the wave; the same holds for its time average. Radiation Pressure: Similarly the pressure exerted on a perfectly absorbing surface by an EM wave is given by P = S/v. E|| is continuous. D⊥ = ε E⊥ changes by σf (if any). B⊥ is continuous. H|| = B||/μ changes by Kf×z (if any). In the case of σf = Kf = 0 (no free charges or currents), all of the components listed above are continuous across the surface. Other universal rules are εμ = 1/v2, v = ω/k and B=E/v As we learned in 1st year, a reflection off a "denser" medium (one with a slower v and therefore a larger index of refraction n) always causes the reflected wave to be π out of phase with the incoming wave. That is, one of E or B must reverse direction on reflection from such a surface, but the other does not. In this case it is B that reverses, while E stays the same. This can be understood in terms of the mechanism for absorption and re-radiation in a dielectric: the incoming E field periodically reverses local electric dipoles along its direction, so the dipoles re-radiate E in that same direction. Conundrum du jour: if the mechanism were mainly working on magnetic dipoles (current loops), would it imply that E would reverse, while B stayed the same? A homework question (9.14) explains why neither field can mix x and y components on reflection or transmission. Bear in mind that the boundary conditions refer to the net fields in any region; on the incoming side that means the sum of the incoming wave's fields and those of the reflected wave. For normal incidence with no free charges or currents, the above boundary conditions require EI + ER = ET and EI - ER = β ET where β equiv; μ1v1/μ2v2 R ≡ SR/SI = [(1-β)/(1+β)]2. T ≡ ST/SI = [(2/(1+β)]2. What if we run it backwards? Simply interchange the subscripts on the media properties. You'll see that this just exchanges β for 1/β and the results for R and T are the same. So (another conundrum) how do 1-way mirrors work? ER/EI = (α - β)/(α + β) and ET/EI = 2/(α + β) Note that as long as β > α, ERET has the opposite sign from EI. This is to say, its phase is flipped by 180o; since the direction of E uniquely determines the direction of B, that means B is not flipped. So there are restrictions on our rule about reflections off a denser medium, at least for the TM case. Small α corresponds to large θI (check it!) so this situation occurs at grazing incidence. At smaller θI there is one particular angle called the Brewster angle [no relation] at which α = β and there is no reflected wave! This angle is a function only of the properties of the media; I won't write out the function here. It is always smaller (closer to the normal) than 45o, the value it takes when the two media are virtually identical. (You can easily show this.) There is no corresponding angle for the TE case, which is why glare (reflections of sunlight off mostly horizontal surfaces) is mostly polarized horizontally: the TM modes are not reflected at angles near the Brewster angle. This is why we wear polarized sunglasses while skiing or fishing: to remove the surviving horizontally polarized reflected glare while letting through any vertically polarized unreflected light. Without such visual aids, "sight fishing" is almost impossible! Following Griffiths I will not derive the TE case for you; but I won't make you do it yourself (Problem 9.16); I'll just give you the answer: ER/EI = (1 - αβ)/(1 + αβ) and ET/EI = 2/(1 + αβ) ∂Ïf/∂t = - (σ/ε) Ïf, with the familiar solution Ïf(t) = Ïf(0) exp(-t/Ï„) where Ï„ = ε/σ. g2 = ω2εμ + i ωσμ where g ≡ k + iκ. The book's formula for φ is tan φ = κ/k, which looks simple until you remember the big ugly formulae for k and κ. Isn't there an easier way? Yes! Recalling our result for g2 in terms of ε, μ, σ and ω, and noting that g2 is also equal to K2 e2iφ, equating the real and imaginary parts of each yields the simple equation tan 2φ = σ/εω. K = k0 [1 + (σ/εω)]1/4 Limiting Cases: g2 = μσω (i + εω/σ) so g = (μσω)1/2 (i + εω/σ)1/2 ≈ (μσω)1/2 (i + εω/2σ). g = (μσω/2)1/2 [(1 + εω/2σ) + i(1 - εω/2σ)]. The simplest possible superposition (two plane waves going in the same direction but with slightly different ω and k) can be written ei[(k+dk)x - (ω+dω)t] + ei[(k-dk)x - (ω-dω)t] = 2ei(kx - ωt) cos[dk{x - (dω/dk)t}]. The argument of the cosine explicitly shows that the nodes of the "beat" pattern in space and time propagate at the group velocity vg ≡ dω/dk, which is the same as vph ONLY if ω is a linear function of k, ω = ck. We are now considering cases where this is not true. σ = q2N/m(γ - iω). σ = iε0ωp2/ω where ωp2 ≡ Nq2/mε0 g2 = (1/c2)(ω2 - ωp2). ε = ε0(1 + χe) = 1 + ωp2[ω02 - ω2 - iωγ]-1. Usually μ ≈ μ0 and |χe| << 1, allowing the approximation (εmu;)1/2 = (1/c)(1 + χe)1/2 ≈ (1/c)(1 + χe/2), giving k + iκ = (ω/c) {1 + (ωp2/2)[(ω02 - ω2 - ω2 - iωγ]-1}. n ≡ ck/ω ≈ 1 + (ωp2/2){(ω02 - ω2)/[(ω02 - ω2)2 + γ2ω2]} α ≡ 2κ ≈ ωp2/c){γω2/[(ω02 - ω2)2 + γ2ω2]} When there are different species with different masses, charges, binding strengths, damping factors or number densities, the factor starting with ωp2 is replaced by a sum over all such species. Now, most ω0's are at quite high frequencies, so we are usually in the low frequency limit (ω << ω0) where there is very little absorption and n is gradually increasing with ω. Near a resonance, however, absorption is strongly peaked in a Lorentzian lineshape and (n - 1) looks like the derivative of a Lorentzian. It may seem alarming that (n - 1) can go negative (implying vph > c), but as we have discussed, neither information nor energy actually move at this phase velocity vph ≡ ω/k; only at the group velocity vg ≡ dω/dk. You might try finding the latter in this case, if you have some spare time. Suppose our wave is reflecting back and forth between two parallel conducting y-z planes separated by a distance a in the x direction. Pick the z direction to be the direction of the component of k0 parallel to the plane surfaces. Thus k0 = kxx + kzz. Following Griffiths' convention I will drop the z subscript on kz and just call it k. Thus ω2/c2 = kx2 + k2, k = (ω/c) cos θ and kx = (ω/c) sin θ. Since we don't actually observe "rays" bouncing back and forth between the plates at angle θ, but rather the standing waves of the resulting interference pattern, it would be nice to eliminate θ from our description. This is already done for kx = mÏ€/a; we can also do it for k = (ω/c) cos θ = (ω/c) (1 - sin2 θ)1/2 or c k = (ω2 - ωm2)1/2 where ωm ≡ mÏ€c/a If ω < ωm then k is imaginary, i.e. the wave cannot propagate, it just decays away. Thus ωm is a lower limit for allowed frequencies in the mth TE mode. As ω approaches ωm from above, the effective phase velocity vph = ω/k diverges! However, as you can easily show, the group velocity vg = dω/dk = c [1 - (ωm/ω)2]1/2 goes to zero as ω approaches ωm from above. This agrees with the more obvious version stated earlier: vg = c cos θ, but without the reference to the "hidden" parameter θ. For a rectangular waveguide we just add a second pair of conducting planes separated by b in the y direction and add an analogous constraint on ky = nÏ€/b to get c k = (ω2 - ωmn2)1/2 where ωmn2 ≡ [(mÏ€c/a)2 + (nÏ€c/b)2]1/2. I didn't quite finish reproducing the derivation of the TE modes in a rectangular waveguide using separation of variables, Bz(x,y) = X(x)•Y(y) = B0 cos(kxx) cos(kyy) where kx = mÏ€/a and ky = nÏ€/b, The other missing derivation (for TM modes) is a homework problem, so there is no need for me to reproduce that. :-) (10.1.2) Gauge Transformations: I went through the entire explanation for why you can add the gradient of any scalar function to A, as long as you simultaneously subtract the time derivative of that same function from V, without affecting E or B (i.e. without changing any physical observables). Such modifications are known as gauge transformations, and they are extremely important, not only in E&M but also in relativistic quantum field theory; but we won't go there now. (10.1.3) Coulomb and Lorentz Gauges: the most familiar "gauges" are the Coulomb gauge, in which the divergence of A is simply set to zero, leaving Poisson's equation the same as for Electrostatics, and the Lorentz gauge, in which the divergence of A is set equal to - (1/c2) dV/dt [that's a partial derivative, of course]. In the Lorentz gauge, our two "ugly" equations involving potentials turn into inhomogeneous wave equations for V (driven by -
We skip the rest of Ch. 10 (e.g. Retarded Potentials) for now. (Ch. 12) Introduction to Relativity: Just enough of an introduction today to speculate on why Griffiths chooses an unpopular convention for the Minkowski metric so that xµ = {-ct, x, y, z} instead of the more conventional version, xµ = {ct, -x, -y, -z} for the covariant 4-vector. As long as you're consistent, it makes no difference; but Griffiths' version requires all Lorentz scalars (inner products of covariant 4-vectors with contravariant partners like xµ = {ct, x, y, z}) to be negative rather than positive. Ugly. More on Wed. I will try to generate such files for every lecture, but sometimes it may all be "blackboard work" which I'll only outline here. Examples discussed today: "Conductors"; "Materials"; Ampere's law; and (in most detail) Faraday's Law - three versions. Work out Problem 7.19 (p. 310) for z=0 (centre of the skinny toroidal solenoid) for simplicity, using this handy equation. (7.3.3 vs. 7.3.5) Maxwell's Equations (see also inside of back cover): There are two sets of equations, one of which describes the effects of linear polarizable and/or magnetic media explicitly. Are they different? No! Both sets are exact and always true. So why bother? Well, the set with H and D have more fields, but less constants; and they remind us to account for those effects. More on this later. Homily about "standing on the shoulders of giants" - that which is "trivial" when you know the answer may seem pretty hard when you don't. There's no shame in looking to see how Griffiths (or Jackson, or Feynman, or Landau & Lifshitz) did it. a*b = a0b0 - a1b1 - a2b2 - a3b3 Events and Light Cones: to keep track of spacetime coordinates it is often convenient to make a graph showing ct along the vertical direction and x along the horizontal. Since Lorentz transformations affect only time and the spatial component parallel to the relative velocity, we can leave the perpendicular spatial components off our diagram (fortunately for our 2-D blackboard!). An observer with a vertical worldline is at rest in the frame for which the diagram is drawn. (Other frames require their own diagrams.) This is an especially handy frame, because we can talk about the time difference dt between two nearby events at the same place (i.e. dx = 0). We call the time interval in this special frame dt = d Lorentz Transformations: I'm not going to try to do the algebra in HTML, but you will remember that those same two events transform under a Lorentz "boost" (into a "primed" frame moving in the x direction at a speed u) to give a nonzero spatial separation and an increased time interval dt' = c2 d ds = (∂s/∂xμ) dxμ e'⊥ = γ(e⊥ + v x B/c) and B'⊥ = γ(B⊥ - v x e/c) Fμν = ∂μAν - ∂νAμ Transforming Fμν: one motive for expressing the fields in manifestly covariant form is so that we can write down their Lorentz transformation properties "elegantly". For a 4-tensor this consists of (F')μν = Λμα Λνβ Fαβ Contracting Fμν with itself yields FμνFμν ∠E2 - c2B2 FμνGμν ∠E • B In the first part, you are indeed simply looking for the right combination of commands in µView, extrema, gnuplot, MatLab and octave that perform a weighted least-squares fit of the data to a straight line (y = p0 + p1 x) and yield the best-fit values of p0 and p1 with the uncertainties ("errors") in each. You will probably need to symmetrize the y uncertainties in the data points and ignore the x uncertainties, unless you want to estimate the effect of the latter in terms of the former. To perform a fit using python, however, you will need to either learn how to use the sophisticated features of the powerful Minuit fitting program from CERN, as provided to python by the PyMinuit package (invoked by "import minuit" in python) or write your own code in python implementing the closed-form solution to the linear fit as described mathematically in the Assignment. Either way there will be code to write. You will probably find the latter approach (writing your own python code) much easier. Just for fun (and to provide a "porting" model for your python code, and to give you a way to check your results), I have implemented this algorithm in PHP. You can copy the file from I showed my code for the former task in the 12:30 lecture. If you choose to tackle pyminuit, you should consult the GoogleDocs documentation on "Getting Started" with pyminuit. You will need to read in the data as usual and supply a bit of code to calculate chi squared, but then you have all the power of MINUIT at your fingertips, as it were. Just follow the "Getting Started" instructions. But even with the best analytical algebra skills and supporting software, sometimes you run into functions whose integrals are not known as analytical expressions; more often, you might just want to know the numerical answer without a lot of rigamarole. For this it is nice to have a quick method for finding the answer numerically to the desired precision. That last phrase is essential! If you want an exact result, only the analytical solution will do. If you only want the result to within a few %, any crude method will serve in most cases. (Another key phrase -- some functions are "pathological" when it comes to numerical integration, and when you encounter those you will need extra tricks. We won't go there.) So what is your first step? Well, pick some N and make your "comb" and sum up the results. That's your result RN. Now, how do you know if it's good enough? Well, first you need to specify a criterion for convergence, call it C, but you need something to compare with RN to decide if you've converged yet -- i.e. if RN is good enough. So, you'll want to store RN in another variable like R_last and then repeat the "comb" sum calculation with a different N -- call it N'. How to choose N'? For simplicity I suggest just multiplying N by 2, but you can use your own judgement. If |RN' - RN| < C, you're done! If not, make N'' still bigger and try again. And so on until two successive approximations differ by less than the specified criterion. Then you're done. Now, what can go wrong with this procedure? Lots of things. If by accident RN and RN' (or any subsequent pair of successive approximations) happen to match (e.g. the first overestimates and the second underestimates on one bin) then the procedure may terminate prematurely; this is rare and is not too problematic. More common is the case where f(x) diverges at some x in your "comb". This can be worked around, but the presence of such divergences means you are going to have a very hard time getting a suitable result. Some functions are, after all, not integrable! How efficient is this procedure? Not very! For one thing, if you use N' = 2 N, each iteration will repeat all the calculations used in the previous iteration. For the purposes of this Assignment, I don't care. Efficiency is not the point at this stage. As soon as you start worrying about efficiency (or, equivalently, accuracy per CPU cycle) there are a huge variety of tricks to improve the algorithm, some of which you will have learned about in your first Calculus course. Feel free to incorporate these if you wish, but do it yourself, don't just call up some function from the MatLab toolbox. (You can do that later, but not for this Assignment, please.) Although a crude and inefficient algorithm will get you full marks on this Assignment, it is worth mentioning that a more elaborate algorithm, which may be tedious to write and debug, is almost always going to be more efficient than the "brute force" version, simply because a clever calculation of what to do next will almost always take less CPU cycles than a whole lot of "brute force" calculations. I can tell lots of stories about people applying for Cray time to run their BASIC programs faster, but I won't. Just remember, ingenuity is much more powerful than a faster computer! The procedure is simple enough: pick a reasonable starting point (e.g. at the minimum of the range, evaluate the function there, and take a small step toward the maximum of the range. Check to see if the function has changed sign. If so, then it must have crossed zero somewhere in between. Do a binary search to see where: reduce the step size by half and go back in the opposite direction until the sign changes again, then repeat. Continue until the step size is less than your convergence criterion. That's one root. Then head on toward the maximum of the range and repeat the process. And so on. Simple, eh? One can imagine slightly better algorithms (it is dumb to turn around and take two half-steps if the first one doesn't "score", because you already know the second on will; but this just costs you one extra calculation per "turnaround", so it's a fine point of optimization. Just get something to work -- but make sure it's your own creation! Last year this course was taught by Matt Choptuik, who is one of the world's most adept masters of Computational Physics. By contrast, I am just a very experienced amateur. If you would like to sample his offerings, please feel free to visit his 2009 PHYS 210 website and in particular his remarkably lucid and complete Introduction to Unix and Linux. Of course, you have to say it right to get the desired results; and any new language is frustrating to learn, especially when your correspondent takes everything you say exactly literally! So we will start simple. It's hard to say where is the best place to start. Assuming you have successfully logged into your workstation, found the Terminal icon and copied it to your Taskbar, clicked on it and are looking at a command prompt, what command should you type first? At least for your first encounter, I suggest "pwd" (for present working directory -- nothing to do with passwords!). Note: unless otherwise specified, every command is terminated with an ENTER or RETURN keystroke, often written " You are Lord of the Manor, and the computer is your extensive and magnificent Estate. In this Estate you can do many things, such as host huge parties and entertain guests with many activities. Whee! Of course, these activities don't organize themselves. In order to even maintain the Estate, much less throw big parties, you need an extensive Staff of highly skilled and hard-working people, all of whom live to carry out your wishes. There are the Drivers, who know how the different Devices work and how to get them to do the necessary tasks; there are the Librarians, who keep your disk directories in order and can almost instantly retrieve the information you want; and many, many others. The problem is, every one of your Staff speaks only a dialect of Geek specialized to their responsibilities. That's a lot of dialects. As Lord of the Manor, you try to learn as many as you can, but their are other demands on your time. What you need is an interpreter, who speaks all the dialects of Geek required to give detailed instructions to your Staff, plus one more dialect especially designed for efficient communication with you, the Lord of the Manor. Enter the Butler, namely your bash shell, who knows what you mean when you say, "Have the formal gardens prepared for a masqued ball on Saturday evening. We shall have about 100 guests." and, more importantly, which of the Staff to go tell what to do next. The Butler's dialect is a little more complex than most of the others, so it is not trivial to learn, but it beats having to learn the dialects of all the rest of the Staff. Now, every Saturday you have a long list of tasks you want the Butler to have done for you, and every Friday you have to go through the same old list again. This is frustrating and inefficient, especially since you sometimes mispronounce a command and get undesired results that are your own fault. So you make up a detailed list, check it carefully, test it a few times, and then write "FRIDAY 1" on the top, give it to the Butler, and say, "From now on, whenever I say, 'FRIDAY 1', I mean for you to have all these instructions carried out." The Butler says, "Very good, ma'am," and you have just taken your first step in learning the art of programming by creating an alias in your bash shell. Finally, let me reiterate last week's metaphor: those of you who have never used anything but a mouse to communicate with your computer are like Lords of the Manor whose communication with the Butler have been limited to pointing at things and snapping your fingers. Since the Butler is very patient and obedient, the annoyance this would create in a human servant has only been manifest in BSOD crashes; but it is clear that you can't expect a very well-run Estate under such a limited chain of command. The rest of the Assignment is an exercise in "copycat programming", which (despite the perjorative-sounding name) is the quickest way to get started on a new language: namely, get a copy of a program someone else wrote -- preferably one which performs a task similar to the one you have in mind -- and adapt it to your purposes by making small incremental changes and seeing the effect. See Summary below. For Part 3, study the ~phys210/bin/fib.sh script until you understand how it works. I suggest to "start at the top" and liberally comment every line as you move down the script, so that there can be no room for uncertainty. You will need to consult various manuals and/or (in desperation) man bash. (Beware! this is a prodigiously long man file and hard to find things in.) For Part 4, modify one part at a time and check the results before modifying the next part. Think carefully about what you are trying to do (a flowchart may be useful) and this will go quicker and easier than you might expect. Part 5 (the PHP version) can probably wait until Thursday; but it is the same idea as Part 4, in a slightly different (and more powerful) language. Most of you have already learned to plot up simple 2D results on a graph with the independent variable ("abscissa", let's call it x) plotted horizontally and the dependent variable ("ordinate", let's call it y) plotted vertically. Most "data points" (xi,yi) include uncertainties (usually only dyi) which are plotted as "error bars". But the independent variable may also have uncertainties dxi, and it is not always (or even often) the case that the positive and negative uncertainties are the same -- we may have asymmetric errors, and they may be extremely important. So even if you already are adept at plotting up your data, there are some new tricks you need to learn.... A student asked after class how to move files between a remote computer and hyper. This was an excellent question that I wish had been asked in class so that everyone might have benefited from the following answer. Two commands are extremely useful for people working on the same thing at home and at UBC: where, as usual, items in square brackets are optional and items enclosed in angle brackets <...> are generic terms, in this case host and/or directory and/or file specifications. scp stands for "secure copy" -- see "man scp". The "-p" is strongly advised, for it says to preserve the file attributes of the source files in the destination. Very advisable. The optional additional "r" stands for recursively, so that you can copy whole directory trees if needed. However, this is usually not such a great idea, as it will expand all symbolic links into real files on the destination, which is usually not what you had in mind! Better for that is rsync, see below. Usually <sourcefiles> refers to the file(s) on your current host (wildcards like "*" are allowed) and <destination> is of the form user@host:~user/filespec or the reverse, with host: = something like hyper.phas.ubc.ca. You will be asked for the password for user. is the best (IMHO) usage of rsync because it checks all ("-a") files in the directory tree starting at <directory>/ on both hosts and updates ("u") on host2 only those that have more recently been modified or created on host1 than on host2, all the way down that directory tree. It also reproduces symbolic links as symbolic links! This is really handy if you keep the same directory structure on your home computer as on your hyper account, which is highly advisable lest you lose track of where you left a file! You should of course use "man rsync" to learn more details; then you may want to set up aliases on both hosts to do it with all the switches and directories carefully spelled out. Note: the "/"s following <host1:directory and <host2:directory are extremely important! Don't leave them off! The presentation on OOP (along with assorted anecdotes, metaphors and philosophical comments) is intended to clarify the differences between "old-fashioned" linear programming and the popular new paradigm of OOP. The problem with OOP (IMHO) is that it is not a language you can learn "once and for all"; no matter how familiar you become with the Classes of Python or Java or PHP or C++ or C-sharp today, a year from now there will be hundreds or thousands of new Classes that do similar things even better. It is a bit like trying to keep your operating system right up-to-date, a process with which almost everyone is familiar and frustrated. Sorry, the price of "the state of the art" is eternal vigilance. But you can always get simple things done simply, if you know how to use simple tools. We will get back to that later. Each talk will be limited to 7 minutes, with 3 minutes for questions, comments, suggestions and queuing up the next talk. The schedule is packed tight, and we cannot run overtime, so you will get absolutely no extra time. At the end of 7 minutes the next talk will be queued up, without exceptions. I wish we could offer more flexibility, but it is not possible. You may want to practice your talk in its entirety in front of friends (or a mirror) to make sure you are under 7 minutes. OK, enough said on that. Obviously this is not enough time to say much or get much feedback. Think of this as an advertisement for your project, an attempt to get other people interested enough to provide some feedback and suggestions. When and how can such feedback and suggestions be collected? I'm so glad you asked! On the PHYS 210 wiki we have a page called "PHYS 210 PROJECTS" where you should open a wiki page just for your own Project. There are examples from previous years there; do it like they did it, only better! This (the wiki business) doesn't have to be done right away, but the sooner you get to it, the sooner you may get useful suggestions (also from me and the TAs) about your Project. This will eventually be a (required) part of your Project, and your comments/suggestions on other people's Projects (which will form part of your Participation mark) should go there too. The title and brief description above have enticed you to sign up for this course, but I really have no idea what you expect or desire from me. An instructor's usual response to such circumstances is to proceed according to the syllabus or the prerequisites for following courses (difficult in this case, as there is neither a syllabus nor any course to follow) or according to whim ("This is what I like to talk about; if they don't like it, tough!") but after 34 years of delivering lectures I've had my fill of playing Expert/Authority figure, and presumably you have no need for me in such a role. So we're going to do it differently. First I need to know a bit about you and your expectations/preferences. Who are you? How much do you already know about Physics? How seriously do you take Poetry? Philosophy? What did you think this course was going to be about? What would you like this course to be about? Do you expect to do any homework? Reading? Do you mind doing some things on the computer? Do you have access to the Web? (If the consensus is negative on the last question, then you are probably not reading this; so you can tell I am hoping to be able to use Web tools with the course.) While I am a tireless advocate for Poetry, I have no credentials as a Poet, and there are bound to be at least some of you who do; so I will never be tempted to speak with Authority about that discipline - all my pronunciamentos will be understood to represent only my own opinion, and counteropinions will be welcome. Just don't go all ad hominum on me, OK? I do have some Physics credentials, however undeserved, and I have a few favourite topics I'd love to weave into the next 7 weeks if I can. I'll list a few of them below and ask you to give me some feedback on which you'd like me to concentrate upon. There's more, of course, but we'll build on your preferences and follow the discussion where it leads. ALTERNATIVES to MONEY: Reflection and Transmission
General review of First Year arguments used in analyzing thin film interference. Derivation of the familiar quarter wave plate criterion for nonreflective lens coatings, etc. We now set out to understand this more thoroughly.
"Reflections on Reflection"
by Jess H. Brewer
on 2006-02-09:
"Oblique Incidence"
by Jess H. Brewer
on 2006-02-21:
"EM Waves in Conductors"
by Jess H. Brewer
on 2006-02-21: Dispersal of Charge
If we combine Ohm's law [Jf = σ E] with the Continuity Equation [∇•Jf = - ∂Ïf/∂t] and throw in Gauss' law [∇•D ≡ ε ∇•E = Ïf], we get Solutions to the Inhomogeneous Wave Equation (IWE)
If we try for a "wavelike" solution to Maxwell's equations, i.e. B = B0 exp[i(gz - ωt)], where I am using g to represent the "complex wave vector" and labelling the direction of propagation z, applying the IWE (which I won't write out again here) yields Phase Lag
Plugging our wavelike solutions into Faraday's law yields, as usual, B = (g/ω) E. But since g is complex, and can therefore be represented as g = K eiφ, we have B = (K/ω) E eiφ. That is, the phase of the oscillatory B field lags behind that of E by the angle φ. This is a little shocking; we have come to expect E and B to always be in phase! Well, when they aren't, they don't get far. Reflection by Conductors
I just gave some introductory remarks about the expected behaviour of a plane wave striking a perfect conductor (σ → ∞) and how this changes if we let σ be finite and look very near the surface with a good microscopic imagination. More on Friday.
"Mirrors"
by Jess H. Brewer
on 2006-02-22:
"Complex Conductivity"
by Jess H. Brewer
on 2006-02-27: Phase Velocity vs. Group Velocity
Please review this subject from previous courses. (I know you've seen it many times already!) The phase velocity vph ≡ ω/k is not actually restricted to values smaller than c, because it describes the speed of propagation of a point of constant phase on a plane wave of unique ω. A plane wave, however, conveys no information! It has been going on forever and will continue to do so forever. If we want to send a signal, we must turn the plane wave on and off, constructing wave packets by superimposing many plane waves of different frequencies and wavevectors. Driving Free Electrons
Suppose we have an oscillating electric field locally driving charge carriers of mass m and charge q: Newton's Second Law says mdv/dt = q E0 e-iωt - m γ v, where γ is a damping rate, which is plausible but difficult to calculate from first principles. A steady-state solution is v = q E/m(γ - iω). Remembering that J ≡ N q v, where N is the number of charge carriers per unit volume, and using Ohm's law to define the conductivity σ, we have the frequency-dependent Drude theory result for the complex conductivity, EM Waves in a Plasma
In a thin plasma we can write the above result as
"Driving Bound Electrons"
by Jess H. Brewer
on 2006-02-27:
"Wave Guides!
by Jess H. Brewer
on 2006-03-01:  "
"
"Waveguides Done Right"
by Jess H. Brewer
on 2006-03-03:
"Cavities and Coax Cables"
by Jess H. Brewer
on 2006-03-06: Resonant Cavities
If you take a hollow rectangular waveguide and close off the ends, only specific frequencies of standing waves will be allowed ("classical quantization"). You have seen this before in other contexts. Other shapes are allowed as well, of course; one favourite is the cylindrical cavity, which (with small holes in the ends to let particles through) is used extensively in linear accelerators (linacs). Coaxial Transmission Lines
Your home is full of these, especially if you have any electronics, a television set, a computer or stereo equipment. As explained in the PDF file, such "coax cables" have the extremely attractive property of transmitting all frequencies at the same propagation speed in a TEM mode -- i.e. they are dispersionless (except for imperfections like finite conductivity and frequency-dependent dielectric constants).
"Potentials, not Fields!"
Topic
Found 1 Lectures on Fri 31 Jan 2025.
"Representations"
by Jess H. Brewer
on 2006-01-20: 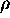 /
/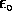 ) and A (driven by -
) and A (driven by -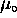 J) which together are equivalent to Maxwell's equations and thus express all of E&M in two equations! Cool, eh?
J) which together are equivalent to Maxwell's equations and thus express all of E&M in two equations! Cool, eh?
"Radiation"
Topic
Found 6 Lectures on Fri 31 Jan 2025.
"Accelerated Charges and Radiation"
by Jess H. Brewer
on 2006-03-20:
"Oscillating Electric Dipole"
by Jess H. Brewer
on 2006-03-26:
"3-Seminar Day"
by Jess H. Brewer
on 2006-03-26:
"Dipole Radiation"
by Jess H. Brewer
on 2006-03-26:
"Radiation from Arbitrary Sources"
by Jess H. Brewer
on 2006-03-27:
"Antennas"
by Jess H. Brewer
on 2006-04-03:
"Retarded Potentials"
Topic
Found 4 Lectures on Fri 31 Jan 2025.
"Retarded Potentials"
by Jess H. Brewer
on 2006-03-06:
"Retarded Potentials, cont'd"
by Jess H. Brewer
on 2006-03-10:
"Jefimenko, Lienard and Wiechert"
by Jess H. Brewer
on 2006-03-16:
"Lienard-Wiechert, cont'd"
by Jess H. Brewer
on 2006-03-20:
"REVIEW"
Topic
Found 6 Lectures on Fri 31 Jan 2025.
"First Lecture"
by Jess H. Brewer
on 2005-12-12:
"Birthday Fiasco"
by Jess H. Brewer
on 2006-01-07:
"Iterations of Truth"
by Jess H. Brewer
on 2006-01-09:
"Review: Media and Other Loose Ends"
by Jess H. Brewer
on 2006-01-11:
"Loose Ends & Review"
by Jess H. Brewer
on 2006-04-03:
"Superconductivity"
by Jess H. Brewer
on 2006-04-03:
"Special Relativity in E&M"
Topic
Found 3 Lectures on Fri 31 Jan 2025.
"4-Vectors & Lorentz Invariants"
by Jess H. Brewer
on 2006-01-24: 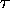 , the proper time interval.
, the proper time interval. 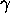 d
d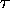 . This is known as time dilation. It is important to remember that is refers to the proper time interval in the frame where the two events are at the same spatial position. Can we generalize d
. This is known as time dilation. It is important to remember that is refers to the proper time interval in the frame where the two events are at the same spatial position. Can we generalize d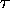 to a quantity that can be defined in any reference frame and that has the same value as that in the rest frame? Of course, or I wouldn't be talking about it.
to a quantity that can be defined in any reference frame and that has the same value as that in the rest frame? Of course, or I wouldn't be talking about it. 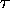 2 = c2dt2 - |dx|2
2 = c2dt2 - |dx|2 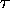 2 in the rest frame where dx = 0. Thus d
2 in the rest frame where dx = 0. Thus d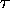 is a Lorentz invariant or a Lorentz scalar, with the lovely property that any 4-vector can be multiplied or divided by it to get a new 4-vector. We will make some use of this on Friday.
is a Lorentz invariant or a Lorentz scalar, with the lovely property that any 4-vector can be multiplied or divided by it to get a new 4-vector. We will make some use of this on Friday.
"More 4-Vectors and Lorentz Scalars"
by Jess H. Brewer
on 2006-01-25:
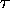 is automatically another 4-vector, because d
is automatically another 4-vector, because d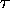 is a Lorentz scalar. The most obvious example is the proper velocity
is a Lorentz scalar. The most obvious example is the proper velocity 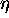 µ = dxµ/d
µ = dxµ/d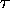 , which therefore transforms "nicely", unlike the ordinary vector velocity v = dx/dt, which transforms "ugly" because both the numerator and the denominator have to be transformed. The components of
, which therefore transforms "nicely", unlike the ordinary vector velocity v = dx/dt, which transforms "ugly" because both the numerator and the denominator have to be transformed. The components of 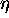 µ are
µ are 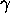 {c, v}. Anyway, if we multiply the proper velocity by another Lorentz scalar, the invariant mass m, we get something more familiar, the 4-momentum pµ =
{c, v}. Anyway, if we multiply the proper velocity by another Lorentz scalar, the invariant mass m, we get something more familiar, the 4-momentum pµ = 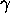 m{ c, v } = { E/c, p }. (Check it!)
m{ c, v } = { E/c, p }. (Check it!) 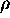 , J }, giving zero as a result. Because it has to be zero in any reference frame (charge conservation is absolute) that is a Lorentz invariant zero, so the product on the left must also be a Lorentz scalar. It is the contraction of one 4-vector (the 4-gradient) with J µ, so J µ must be a 4-vector too! This is a very powerful statement, considering the simplicity of its justification.
, J }, giving zero as a result. Because it has to be zero in any reference frame (charge conservation is absolute) that is a Lorentz invariant zero, so the product on the left must also be a Lorentz scalar. It is the contraction of one 4-vector (the 4-gradient) with J µ, so J µ must be a 4-vector too! This is a very powerful statement, considering the simplicity of its justification.
"Covariant Representations of Electromagnetism"
by Jess H. Brewer
on 2006-01-27: 12.3.2 HOW THE FIELDS TRANSFORM
Griffiths shows several other cases (pp. 522-531) that are summarized in Eqs. (12.108) on p. 531. These equations say that components of E and B parallel to the boost are unchanged, while the components perpendicular to the boost transform as MANIFESTLY COVARIANT NOTATION
After all this indoctrination into the wonders of 4-vectors and Lorentz invariants, we'd like to convert the above description into something more covariant looking. The problem, of course, is that we have six components to transform, and none of them are particularly "timelike" at first glance. This can't be expressed in one 4-vector, obviously, and two 4-vectors give too many components, so we have to go to the next more elaborate entity: a 4-tensor. Now, a general 4-tensor has 16 independent components (too many!) and a symmetric one still has 10 (too many), but an antisymmetric 4-tensor has ony 6 -- just the right number! So let's try to use our favourite 4-vectors ∂μ and Aμ to build an antisymmetric 4-tensor Fμν. Our first guess is
"UBC Physics 210 [Fall 2006]"
Course
"Introduction"
Topic
Found 2 Lectures on Fri 31 Jan 2025.
"Welcome to Physics 210!"
by Jess H. Brewer
on 2006-09-08:
"Login, Profile and Survey"
by Jess H. Brewer
on 2006-09-08:
"Linux and Unix"
Topic
Found 4 Lectures on Fri 31 Jan 2025.
"E-mail, Text Files and Editors"
by Jess H. Brewer
on 2006-09-19:
"HTML and the Web"
by Jess H. Brewer
on 2006-09-19:
"Aliases and Shell Scripts"
by Jess H. Brewer
on 2006-09-19:
"Miscellaneous"
by Jess H. Brewer
on 2006-09-19:
"UBC Physics 438"
Course
"UBC Physics 210"
Course
"Fitting Data to a Theory"
Topic
Found 4 Lectures on Fri 31 Jan 2025.
"Chi Squared Minimization"
by Jess H. Brewer
on 2010-10-16: ~phys210/public_html/linfit.php if you like.
"Fitting in Python"
by Jess H. Brewer
on 2010-10-25:
"FORTRAN"
by Jess H. Brewer
on 2010-10-25:
"Errors, Issues & Announcements"
by Jess H. Brewer
on 2010-10-28:
"Good Approximations"
Topic
Found 2 Lectures on Fri 31 Jan 2025.
"Numerical Integration"
by Jess H. Brewer
on 2010-11-23:
"Thanks for all the Fish!"
by Jess H. Brewer
on 2010-11-25:
"Introduction"
Topic
Found 5 Lectures on Fri 31 Jan 2025.
"Welcome to Physics 210!"
by Jess H. Brewer
on 2010-09-05:
"Get Ready.. Get Set Up... Go!"
by Jess H. Brewer
on 2010-09-14:
"Lord of the Manor"
by Jess H. Brewer
on 2010-09-16:
"Backups, Images and Shell Scripts"
by Jess H. Brewer
on 2010-09-20:
"Flowcharts & PHP"
by Jess H. Brewer
on 2010-09-22:
"Linear Algebra"
Topic
Found 1 Lectures on Fri 31 Jan 2025.
"Spin and the Pauli Matrices"
by Jess H. Brewer
on 2010-11-17:
"Plotting Data"
Topic
Found 3 Lectures on Fri 31 Jan 2025.
"Doing it Many Ways"
by Jess H. Brewer
on 2010-09-26:
"Odds & Ends"
by Jess H. Brewer
on 2010-10-01:
"Python"
by Jess H. Brewer
on 2010-10-01:
"Presentations"
Topic
Found 1 Lectures on Fri 31 Jan 2025.
"Projects, Proposals & Presentations"
by Jess H. Brewer
on 2010-10-06:
"Project Week"
Topic
Found 1 Lectures on Fri 31 Jan 2025.
"Project Week"
by Jess H. Brewer
on 2010-11-17:
"Typesetting with REVTeX4"
Topic
Found 1 Lectures on Fri 31 Jan 2025.
"Typesetting with REVTeX4"
by Jess H. Brewer
on 2010-11-17:
"Physics, Poetry & Philosophy"
Course
"Introduction"
Topic
Found 1 Lectures on Fri 31 Jan 2025.
"Introduction"
by Jess H. Brewer
on 2015-11-27:
"Possible Futures"
Course
"Artificial [General] Intelligence"
Topic
Found 1 Lectures on Fri 31 Jan 2025.
"AI & AGI"
by Jess H. Brewer
on 2017-11-06:
"Future Economics"
Topic
Found 1 Lectures on Fri 31 Jan 2025.
"Economics of the Future"
by Jess H. Brewer
on 2017-11-28:
JOBS: Speaking of robots doing everything for us... during the transition from {endless human toil & compensation therefor} to {a world of plenty provided by robots}, the robots will be seen (rightly enough) to be "taking away the jobs that we need to feed our families". One may view this as the fault of those who collect the fruits of the robots' labor to augment their own wealth rather than to provide for the newly unemployed. Is there any way to make it through this transition peacefully? Another question: if all the work is done for free and we have everything we need without money or employment, what will we do with our time? Will we lose our initiative, or even our will to live and reproduce, without the challenges of scarcity? This reminds me of last week's ultimate question: if we could really reverse aging, cure all diseases and live healthy forever, would we want to? (I would, but that's just me. :-)
Looking at the state of JOBS in the present, there are interesting articles in the Huffington Post and the Globe & Mail, respectively, about the difference between unemployment & underemployment backed up by census data that speak to the above trend.
Artists are one group whose "employment" is already extremely tenuous; trying to survive on intermittent cash injections, they have formed an informal "sharing economy" to try to keep each other afloat. My daughter agrees with this article in The Walrus that the new Creative Canada policy is an attempt to "monetize" art, redefining it in Silicon Valley terms (artists are now "content creators") and "imagines culture as something you stream on Netflix." Thus artists will have to be among the first to find a new paradigm for "labor" and "compensation".
It's also evident to me that this is one topic where we will likely have clear arguments for pessimism vs. optimism, so maybe we should keep score somehow. :-)
TECHNICAL FIXES:
Many people feel that an enlightened dictatorship is the ideal form of government. (The problem is with maintaining the enlightenment of the dictator.) Others treasure liberty over all other political values. (Subject of course to the dictum that, "Your liberty to swing your fist ends at the tip of my nose.") Genuine democracy always means having to live with the bad decisions of the ignorant and misguided, whereas a republic relies upon uncorrupted good faith in the selection of the wisest among us at each level of the representation hierarchy. Can we imagine a system of nominally total freedom monitored and regulated by wise and powerful AGIs with no axes of their own to grind? Would we submit to it?
My daughter has once again pointed out that all these "technical fixes" are fraught with dangers at least as scary as the road we're already on. I can't deny it, but these are just propositions, not plans. A lot of work needs to be done before any of them could be attempted, and most will probably be abandoned due to fatal flaws; but doing nothing is not an option.
5-minute bathroom break!
And now let's choose a topic for next week. Anyone want to add to the list in the syllabus?
A good place to start is to tell my life story, in as compact terms as possible; I believe this will help you decide which of my opinions to take with how many grains of salt.
In the summer of 1945, nuclear weapons were used for the first (and hopefully last) time to kill large numbers of humans and destroy the two cities of Hiroshima and Nagasaki. Half a year later, I was born in Orlando, Florida to a Floridian mother and a Texan father.
Skip forward a decade to the two years (4th and 5th grades) I spent in Lincoln, Nebraska -- 50 miles northeast of SAC Headquarters in Omaha. Every week or two we would get a lecture from a Civil Defense agent describing in gruesome detail how we should duck and cover when we see the fireball of the inevitable Soviet H-bomb and what would probably happen next. Since millions of other kids got the same lecture, I do have a personal understanding of why so many Boomers suffer from Nuclear PTSD.
As a teenager I read every SF novel about the Nuclear Apocalypse and watched all the movies, especially "On the Beach", whose premise I took at face value. I was less gullible about the radioactive spiders in Holywood movies, but when my boarding school classmates set off a flashbulb outside my dorm room during the Cuban Missile Crisis, I rewarded them with the desired reaction of abject terror.
In college I majored in Physics and minored in Creative Writing, planning to become a science fiction author. In 1967 I applied to Berkeley for grad school in Physics, hoping to get a PhD for real credibility! But in the process I discovered µSR, which was like being a character in my own SF story!
The next thing I knew I was 65 and still hadn't written that novel, so I retired in 2011 and moved to Nanoose Bay a year later. Novel-writing turned out to be harder than I thought, so now I content myself with teaching VIU Elder College courses on subjects I don't really understand much better than my students.
Oh, wait... I left out the most important part: at Berkeley I got a job working at the "Rad Lab" (now Lawrence Berkeley National Laboratory) as a junior grad student on a particle physics experiment at the Bevatron, where I met lots of famous people, including my friend Bob Budnitz (who became famous later). Bob was a particle physicist by training, but when his postdoc appointment at LBL ended he descided to switch fields to the new Energy & Environment Division, where he produced the "Big Blue Book" on Radiation Safety.
Later Bob went to Washington, DC, to run the Research Division of the Nuclear Regulatory Agency (NRC) and help prevent the Three Mile Island meltdown from becoming a more serious accident. Under Bob the safety of reactors improved by several orders of magnitude, thanks to a strict policy of shutting down and doing a meticulous analysis of every hiccup of even the most innocuous sort.
The most poignant memory I have of those years was when Bob resigned from the NRC after a meeting with leaders of the antinuke movement in which they explained that their main goal was to prevent him from doing the research that would make reactors safer.
Years later, in the late 1970s, I had a similar conversation with an antinuke organizer in Vancouver: I explained that nuclear power was the only obvious way we could replace the burning of fossil fuels for electrical power, which (we knew even then) would eventually cause a runaway Greenhouse Effect that might sterilize the planet. He replied, "I know that. But at least it would be natural." In his irrationality I thought I detected the same PTSD that I had suffered from growing up in the Cold War. But why was I still able to be rational about it, while he was not? I still have no answer, and the current US elections don't help!