THE UNIVERSITY OF BRITISH COLUMBIA
Physics 108
Assignment #
12
SOLUTIONS:
DIFFRACTION
Wed. 30 Mar. - finish by Wed. 6 Apr. 2005
- SOUND DIFFRACTION:
You are standing
30
m away from a large, soundproof building,
directly in front of a
1
m wide doorway, when it opens and you hear
someone blowing a loud whistle at a frequency of
1320
Hz from somewhere directly behind the door,
deep inside the building.
How far sideways (parallel to the wall with the door in it)
must you move before the sound first becomes imperceptible?
[Assume that the speed of sound is 343 m/s.]
ANSWER: The wavelength
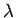 of the sound waves is given by
of the sound waves is given by
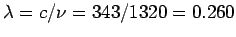 m, where
m, where 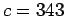 m/s.
The door ("slit") is narrow compared with its distance from
the source deep inside the building, so
we may treat it as uniformly illuminated by plane waves.
The sound will first become imperceptible at the position of
the first minimum of the diffraction pattern.
Thus we need to find
m/s.
The door ("slit") is narrow compared with its distance from
the source deep inside the building, so
we may treat it as uniformly illuminated by plane waves.
The sound will first become imperceptible at the position of
the first minimum of the diffraction pattern.
Thus we need to find
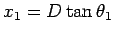 ,
where
,
where
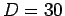 m.
This is where
m.
This is where
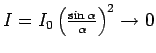 ,
i.e. where
,
i.e. where
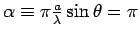 or where
or where
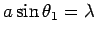 , giving
, giving
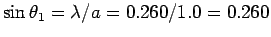 or
or
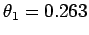 radian (15.06
radian (15.06 ),
not a particularly small angle.
Thus
),
not a particularly small angle.
Thus
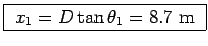 is the position in question.
is the position in question.
- 10-SLIT MINI-GRATING:
Consider a series of
10
equal slits, each
0.004
cm wide, arrayed in a straight line
with equal spacing so that
0.22
cm separates the centres of the first and last slits.
This configuration is illuminated from behind by a
distant source of light of wavelength
0.546
microns [
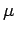 m].
m].
- How many major intensity peaks will you see
in the entire pattern displayed on a wide screen
20
m away before the pattern first fades away laterally
because of the diffraction from each aperture?
ANSWER: The first minimum of the DIFFRACTION envelope
occurs at an angle
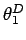 given by
given by
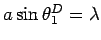 ;
meanwhile, the principal maxima of the
;
meanwhile, the principal maxima of the 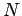 -slit
INTERFERENCE pattern occur at angles
-slit
INTERFERENCE pattern occur at angles 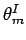 given by
given by
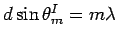 . The question then becomes,
"What is the largest
. The question then becomes,
"What is the largest 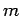 for which
for which
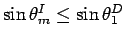 ?"
If we treat
?"
If we treat 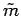 as a continuous variable, we can solve for
as a continuous variable, we can solve for
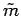 by setting
by setting
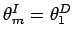 :
:
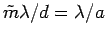 or
or
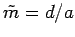 . In this case,
. In this case,
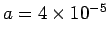 m and
m and
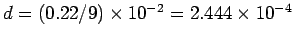 m, so that
m, so that
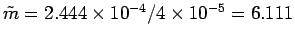 and thus the largest integer
and thus the largest integer 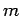 is
is
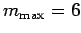 , giving
, giving
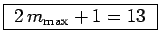 peaks in the region specified.
Note that neither the distance to the screen nor the wavelength of the light
(as long as it is small compared to
peaks in the region specified.
Note that neither the distance to the screen nor the wavelength of the light
(as long as it is small compared to 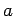 ) is relevant to the answer.
) is relevant to the answer.
- How far apart and how wide1 (in mm) are the principal2 maxima near the centre of the screen?
ANSWER: The angles
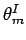 at which principal maxima occur
are given by
at which principal maxima occur
are given by
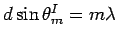 . Thus the
angular separation
. Thus the
angular separation 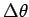 between the central maximum
and the first principal maximum of the interference pattern is
given by
between the central maximum
and the first principal maximum of the interference pattern is
given by
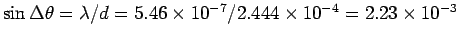 or
or
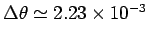 radians. (The small-angle approximation is excellent here.)
The width of each principal maximum is
radians. (The small-angle approximation is excellent here.)
The width of each principal maximum is 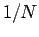 of the distance
between them:
of the distance
between them:
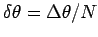 . Here
. Here 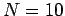 , giving
, giving
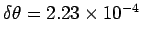 radians. Now, to translate this into positions on a screen
radians. Now, to translate this into positions on a screen 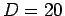 m away we must multiply
m away we must multiply 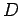 by
by
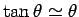 ,
giving a distance
,
giving a distance
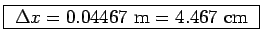 between principal maxima of width
between principal maxima of width
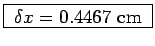 .
.
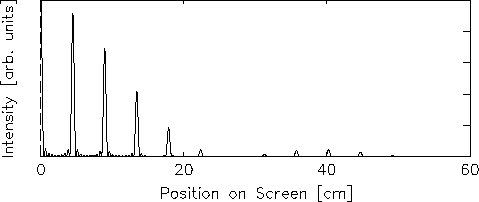
- Sketch the intensity pattern from the central maximum
out to the second diffraction minimum on one side.
ANSWER: You now have everything you need to make the sketch:
- DIFFRACTION-LIMITED VISION:
In fairly bright light the pupil of your eye will contract
to a diameter of about 4 mm. Under these conditions,
assuming that you have "perfect" vision,
- how far from your eye can you hold a book
and still be able to resolve two black dots separated by
100
 m,
illuminated by yellow light with
m,
illuminated by yellow light with 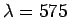 nm?
ANSWER: The RESOLUTION FUNCTION
nm?
ANSWER: The RESOLUTION FUNCTION 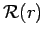 of a DETECTOR receiving a signal from
a point source at distance
of a DETECTOR receiving a signal from
a point source at distance 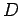 is the same thing as the INTENSITY distribution
is the same thing as the INTENSITY distribution 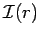 from a SOURCE of the same size and shape at that distance.
The dots are resolvable if the first minimum of
from a SOURCE of the same size and shape at that distance.
The dots are resolvable if the first minimum of 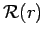 centred on one dot coincides with the location of the second dot
a transverse distance
centred on one dot coincides with the location of the second dot
a transverse distance 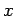 away.
That is (by the RAYLEIGH CRITERION), if
away.
That is (by the RAYLEIGH CRITERION), if
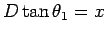 where
where
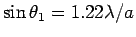 ,
,
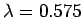
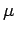 m and
m and 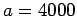
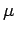 m is the diameter of the circular aperture (your pupil).
This gives
m is the diameter of the circular aperture (your pupil).
This gives
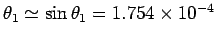 radian, corresponding to
radian, corresponding to 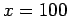
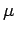 m at a distance
m at a distance 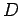 given by
given by
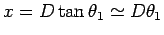 or
or
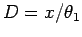 , in this case
, in this case
 .
.
- Describe what you would see at this distance
when observing a single white dot on a black page
illuminated with white light (all wavelengths).
ANSWER: The analysis above predicts that yellow light
from such a dot at that distance
will produce a diffraction pattern on your retina
that makes the dot look smeared out over a radius
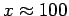
 m on the page. This radius will be proportionally larger
for longer wavelengths (red light) and smaller for shorter
wavelengths (blue light). All wavelengths will have a
central maximum at the same place, so the centre of the
dot will appear white; but the blue wavelengths drop off
at shorter radii, leaving a reddish halo growing redder and
dimmer as the blue components reach their first minimum at
about
m on the page. This radius will be proportionally larger
for longer wavelengths (red light) and smaller for shorter
wavelengths (blue light). All wavelengths will have a
central maximum at the same place, so the centre of the
dot will appear white; but the blue wavelengths drop off
at shorter radii, leaving a reddish halo growing redder and
dimmer as the blue components reach their first minimum at
about
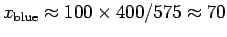
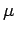 m, after which the red component continues to decrease
toward
m, after which the red component continues to decrease
toward
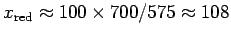
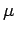 m, at which point the blue has partially recovered; and so on.
Of course, the intensity drops off rapidly away from the central maximum,
so all you can really hope to see is a white centre with a reddish halo about
140
m, at which point the blue has partially recovered; and so on.
Of course, the intensity drops off rapidly away from the central maximum,
so all you can really hope to see is a white centre with a reddish halo about
140
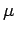 m in diameter surrounded by a fainter bluish halo
at nearly twice that diameter.
m in diameter surrounded by a fainter bluish halo
at nearly twice that diameter.
Jess H. Brewer
2005-03-20
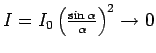 ,
i.e. where
,
i.e. where
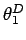 given by
given by
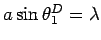 ;
meanwhile, the principal maxima of the
;
meanwhile, the principal maxima of the 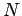 -slit
INTERFERENCE pattern occur at angles
-slit
INTERFERENCE pattern occur at angles 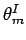 given by
given by
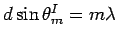 . The question then becomes,
"What is the largest
. The question then becomes,
"What is the largest 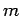 for which
for which
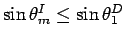 ?"
If we treat
?"
If we treat 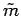 as a continuous variable, we can solve for
as a continuous variable, we can solve for
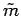 by setting
by setting
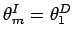 :
:
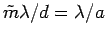 or
or
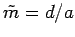 . In this case,
. In this case,
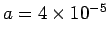 m and
m and
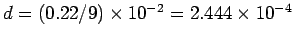 m, so that
m, so that
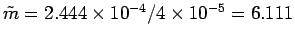 and thus the largest integer
and thus the largest integer 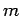 is
is
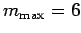 , giving
, giving
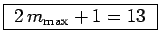 peaks in the region specified.
Note that neither the distance to the screen nor the wavelength of the light
(as long as it is small compared to
peaks in the region specified.
Note that neither the distance to the screen nor the wavelength of the light
(as long as it is small compared to 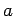 ) is relevant to the answer.
) is relevant to the answer.
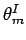 at which principal maxima occur
are given by
at which principal maxima occur
are given by
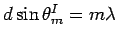 . Thus the
angular separation
. Thus the
angular separation 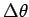 between the central maximum
and the first principal maximum of the interference pattern is
given by
between the central maximum
and the first principal maximum of the interference pattern is
given by
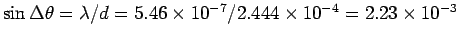 or
or
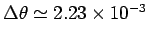 radians. (The small-angle approximation is excellent here.)
The width of each principal maximum is
radians. (The small-angle approximation is excellent here.)
The width of each principal maximum is 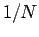 of the distance
between them:
of the distance
between them:
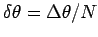 . Here
. Here 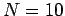 , giving
, giving
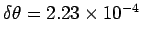 radians. Now, to translate this into positions on a screen
radians. Now, to translate this into positions on a screen 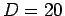 m away we must multiply
m away we must multiply 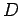 by
by
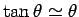 ,
giving a distance
,
giving a distance
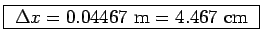 between principal maxima of width
between principal maxima of width
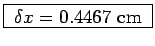 .
.

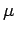 m,
illuminated by yellow light with
m,
illuminated by yellow light with 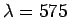 nm?
ANSWER: The RESOLUTION FUNCTION
nm?
ANSWER: The RESOLUTION FUNCTION 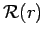 of a DETECTOR receiving a signal from
a point source at distance
of a DETECTOR receiving a signal from
a point source at distance 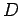 is the same thing as the INTENSITY distribution
is the same thing as the INTENSITY distribution 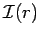 from a SOURCE of the same size and shape at that distance.
The dots are resolvable if the first minimum of
from a SOURCE of the same size and shape at that distance.
The dots are resolvable if the first minimum of 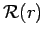 centred on one dot coincides with the location of the second dot
a transverse distance
centred on one dot coincides with the location of the second dot
a transverse distance 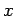 away.
That is (by the RAYLEIGH CRITERION), if
away.
That is (by the RAYLEIGH CRITERION), if
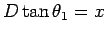 where
where
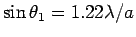 ,
,
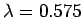
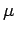 m and
m and 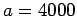
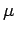 m is the diameter of the circular aperture (your pupil).
This gives
m is the diameter of the circular aperture (your pupil).
This gives
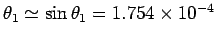 radian, corresponding to
radian, corresponding to 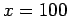
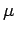 m at a distance
m at a distance 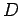 given by
given by
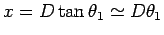 or
or
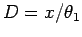 , in this case
, in this case
 .
.
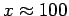
 m on the page. This radius will be proportionally larger
for longer wavelengths (red light) and smaller for shorter
wavelengths (blue light). All wavelengths will have a
central maximum at the same place, so the centre of the
dot will appear white; but the blue wavelengths drop off
at shorter radii, leaving a reddish halo growing redder and
dimmer as the blue components reach their first minimum at
about
m on the page. This radius will be proportionally larger
for longer wavelengths (red light) and smaller for shorter
wavelengths (blue light). All wavelengths will have a
central maximum at the same place, so the centre of the
dot will appear white; but the blue wavelengths drop off
at shorter radii, leaving a reddish halo growing redder and
dimmer as the blue components reach their first minimum at
about
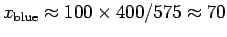
 m, after which the red component continues to decrease
toward
m, after which the red component continues to decrease
toward
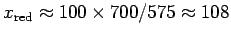
 m, at which point the blue has partially recovered; and so on.
Of course, the intensity drops off rapidly away from the central maximum,
so all you can really hope to see is a white centre with a reddish halo about
140
m, at which point the blue has partially recovered; and so on.
Of course, the intensity drops off rapidly away from the central maximum,
so all you can really hope to see is a white centre with a reddish halo about
140
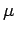 m in diameter surrounded by a fainter bluish halo
at nearly twice that diameter.
m in diameter surrounded by a fainter bluish halo
at nearly twice that diameter.