Making use of the EQUIPARTITION THEOREM, derive an equation analogous to the familiar 3D IDEAL GAS LAW (
ANSWER:
The arguments developed for the time-averaged force
exerted on one wall of a cubical 3D container apply equally well
for the force acting on the boundary of a 1D ``box'' - namely,
for a single particle bouncing back and forth,
![]() ,
where L is the length of the ``box''.
In this case there is only one direction of motion
(degree of freedom) so we can drop the x subscript on vx.
The EQUIPARTITION THEOREM says that the thermal
average of the kinetic energy
,
where L is the length of the ``box''.
In this case there is only one direction of motion
(degree of freedom) so we can drop the x subscript on vx.
The EQUIPARTITION THEOREM says that the thermal
average of the kinetic energy
![]() associated with
this translational degree of freedom is
associated with
this translational degree of freedom is
![]() , giving
, giving
![]() .
If we substitute this back into the formula for
.
If we substitute this back into the formula for
![]() we get
we get
![]() . For N particles all
doing this at the same time, we just multiply by N, giving
. For N particles all
doing this at the same time, we just multiply by N, giving
![]() or (ignoring the fact that the
actual force F at any instant fluctuates minutely about the average
force
or (ignoring the fact that the
actual force F at any instant fluctuates minutely about the average
force
![]() )
)
![]() .
This is the 1D equivalent of the IDEAL GAS LAW.
Note that the only difference between this derivation and the one for
a 3D box is that here we didn't have to introduce the notion of
pressure as the force per unit area. This is simpler!
.
This is the 1D equivalent of the IDEAL GAS LAW.
Note that the only difference between this derivation and the one for
a 3D box is that here we didn't have to introduce the notion of
pressure as the force per unit area. This is simpler!
- (a)
- What is the thermal speed distribution
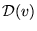 [in the textbook's notation, N(v)/N, as in Eq. (22-14) on p. 503]
for an ideal gas confined to a one-dimensional ``box''?
It would be nice if you could find the right leading factors
(involving temperature and various constants)
to normalize the distribution so that
[in the textbook's notation, N(v)/N, as in Eq. (22-14) on p. 503]
for an ideal gas confined to a one-dimensional ``box''?
It would be nice if you could find the right leading factors
(involving temperature and various constants)
to normalize the distribution so that
but I am mainly looking for its dependence on the speed v.
Hint: Use de Broglie's hypothesis (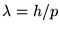 )
and think in terms of standing waves.
)
and think in terms of standing waves.
ANSWER: Again the 1D case is much simpler than the 3D case because we don't have to worry about composing v2 out of vx2 + vy2 + vz2 (or
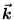 out of kx, ky and kz).
There is just one direction, just one velocity component,
one momentum component and one wavelength to worry about
making commensurate with the length of the ``box''.
Thus the requirement that an integer n half-wavelengths
fit evenly into
out of kx, ky and kz).
There is just one direction, just one velocity component,
one momentum component and one wavelength to worry about
making commensurate with the length of the ``box''.
Thus the requirement that an integer n half-wavelengths
fit evenly into 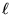 gives
gives
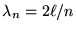 and so
and so
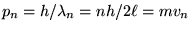 or
or
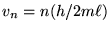 . Thus the possible values of
the speed v are evenly spaced every
. Thus the possible values of
the speed v are evenly spaced every
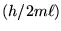 and the distribution of speeds varies only as the
Boltzmann factor
and the distribution of speeds varies only as the
Boltzmann factor
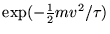 . This gives immediately
. This gives immediately
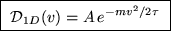 where A is a normalization constant that does not depend on v.
You get full credit for this result, but here's how to get A:
Let
where A is a normalization constant that does not depend on v.
You get full credit for this result, but here's how to get A:
Let
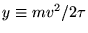 where
where 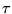 is treated as a constant.
Now,
is treated as a constant.
Now,
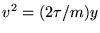 or
or
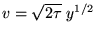 so
so
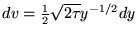 and we have
and we have
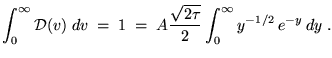 You can look up the definite integral; its value is
You can look up the definite integral; its value is
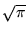 ,
giving
,
giving
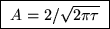 .
.
Woops! Did anyone notice my mistake? There is a square root of m missing. See if you can find where it belongs.
- (b)
- Sketch this distribution for a given temperature
and compare its shape with that shown in the Figures
on p. 503 of the textbook.
ANSWER:
3D:
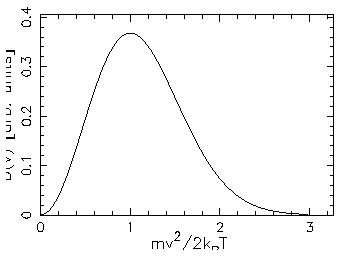
1D:
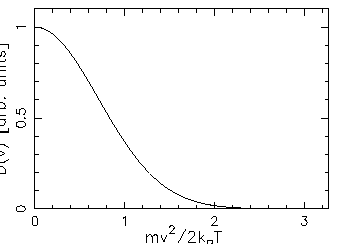
- (c)
- What can you say about the most probable speed
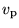 in the two different cases?
in the two different cases?
ANSWER: As stated in the textbook, the most probable speed for an ideal gas molecule in 3D is
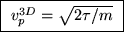 (i.e. when
(i.e. when
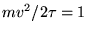 ).
For the 1D gas, however,
).
For the 1D gas, however,
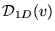 is missing that
extra factor of v2 that forces its value to zero at v=0,
so the resultant speed distribution has its maximum
at v=0:
is missing that
extra factor of v2 that forces its value to zero at v=0,
so the resultant speed distribution has its maximum
at v=0:
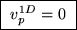 .
.
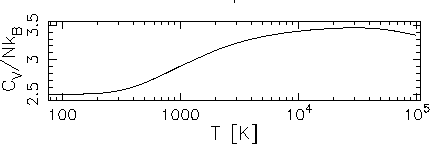
Sketch (including axis labels and scales) the heat capacity per molecule, C1, of an ideal gas of diatomic nitrogen (N2) molecules in an isolated closed vessel of fixed volume, as a function of temperature
ANSWER:
The qualitative picture was drawn in class; this is all about
quantitative estimates of how hot the gas has to get before
rotational and vibrational degrees of freedom are excited.
For this you need to remember that (i) the energy of either
is always given by
![]() where
where
![]() J-s; and
(ii) that the lowest nonzero angular momentum allowed
for any object (including a molecule) is
J-s; and
(ii) that the lowest nonzero angular momentum allowed
for any object (including a molecule) is
![]() .
You already know how to find the resonant frequency of a pair
of masses connected by a spring; you need only the effective
``spring constant'' for the N2 bond, namely
.
You already know how to find the resonant frequency of a pair
of masses connected by a spring; you need only the effective
``spring constant'' for the N2 bond, namely
![]() N/m,
and the mass of a 14N atom:
N/m,
and the mass of a 14N atom:
![]() kg.
So
kg.
So
![]() s-1. The corresponding energy is
s-1. The corresponding energy is
![]() giving
giving
![]() .
At lower temperatures the vibrational degrees of freedom
will not be thermally excited.
Now for the rotational ones: the distance between the two
14N nuclei in an N2 molecule is about 1 Å
.
At lower temperatures the vibrational degrees of freedom
will not be thermally excited.
Now for the rotational ones: the distance between the two
14N nuclei in an N2 molecule is about 1 Å
![]() m.
Crudely representing the molecule as two point masses an Angstrom apart,
the moment of inertia is about
m.
Crudely representing the molecule as two point masses an Angstrom apart,
the moment of inertia is about
![]() J-s2. Now,
J-s2. Now,
![]() gives
gives
![]() s-1 and so
s-1 and so
![]() J.
A state with this size energy will get excited only if the temperature
is comparable to or greater than
J.
A state with this size energy will get excited only if the temperature
is comparable to or greater than
![]() or
or
![]() K. Hmm, looks like I was mistaken when I said in class
that the rotational degrees of freedom are only excited at high
temperature. Considering that nitrogen freezes solid at 68 K,
it is safe to say that N2 gas has its rotational
heat capacity at all temperatures, giving a total heat capacity of
K. Hmm, looks like I was mistaken when I said in class
that the rotational degrees of freedom are only excited at high
temperature. Considering that nitrogen freezes solid at 68 K,
it is safe to say that N2 gas has its rotational
heat capacity at all temperatures, giving a total heat capacity of
![]() from
room temperature up to about 900 K, and then
from
room temperature up to about 900 K, and then
![]() .
The binding energy of an N2 molecule is around 11 eV
(or
.
The binding energy of an N2 molecule is around 11 eV
(or
![]() J) so at temperatures above about
J) so at temperatures above about
![]() the molecules will
dissociate into nitrogen atoms. Then each atom will contribute
only its translational degrees of freedom, giving
the molecules will
dissociate into nitrogen atoms. Then each atom will contribute
only its translational degrees of freedom, giving
![]() .
(I'm not sure I believe this myself; at any rate the atoms are
apt to ionize by that temperature.)
Sketch: 1
.
(I'm not sure I believe this myself; at any rate the atoms are
apt to ionize by that temperature.)
Sketch: 1