| y [m] | Fh [beats/min] | avg. speed [m/s] | ratio CDy/CD3 | ||
| 0 | 25 | 26.24 | 140 | 0.953 | 1.282 |
| 0 | 25 | 26.37 | 136 | 0.948 | 1.295 |
| 0.5 | 25 | 25.45 | 140 | 0.982 | 1.206 |
| 0.5 | 25 | 25.15 | 140 | 0.994 | 1.178 |
| 1.0 | 25 | 23.85 | 140 | 1.048 | 1.059 |
| 1.0 | 25 | 27.73 | 140 | 0.902 | 1.432 |
| 1.5 | 25 | 22.95 | 144 | 1.089 | 0.981 |
| 1.5 | 25 | 22.95 | 140 | 1.089 | 0.981 |
| 2.0 | 22.86 | 21.90 | 140 | 1.044 | 1.068 |
| 2.0 | 22.86 | 21.56 | 144 | 1.060 | 1.035 |
| 2.5 | 22.86 | 21.60 | 140 | 1.058 | 1.039 |
| 2.5 | 22.86 | 21.44 | 140 | 1.066 | 1.024 |
| 3.0 | 22.86 | 21.15 | 136 | 1.081 | 0.996 |
| 3.0 | 22.86 | 21.23 | 140 | 1.077 | 1.004 |
- Calculate the average speed for each lap.
ANSWER:
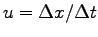 . See the table above and the graph below.
. See the table above and the graph below.

- Assume a body shape like a flattened torpedo
of cross section area A = 0.07 m2,
and a drag coefficient
CD3 = 0.05
to calculate the average drag force F3 at a depth of y = 3.0 m.
This is also the average propulsion force generated by the swimmer.
ANSWER:
The Reynolds number for such a shape is given by
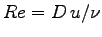 , where
, where
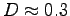 m is the diameter of the torpedo,
m is the diameter of the torpedo,
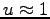 m/s is a typical velocity and
m/s is a typical velocity and
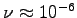 m2/s
is the kinematic viscosity of water
(from Table 3.4 on p. 86 of the textbook).
Thus
m2/s
is the kinematic viscosity of water
(from Table 3.4 on p. 86 of the textbook).
Thus
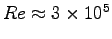 and the flow is very turbulent,
so that most of the drag is hydrodynamic drag
and we can ignore laminar drag (skin friction).
According to Fig. 3.18 on p. 92 of the textbook,
this is just the range of Re in which the drag coefficient CD
suddenly begins to drop with increasing Re.
Therefore we should expect dramatic differences between
swimming speeds of athletes with only slightly different thrust.
However, the depth dependence is primarily due to
ventilation drag and/or wave drag,
as shown in Fig. 3.22 on p. 95.
The swimmer (even underwater) creates a wave that travels with her,
and must push along the "hump of water" that results;
the size of this "hump" decreases as she gets further from the surface.
Once she is far enough below the surface that we can ignore this effect,
we should be able to use Boye's formula on p. 93 for the hydrodynamic drag:
and the flow is very turbulent,
so that most of the drag is hydrodynamic drag
and we can ignore laminar drag (skin friction).
According to Fig. 3.18 on p. 92 of the textbook,
this is just the range of Re in which the drag coefficient CD
suddenly begins to drop with increasing Re.
Therefore we should expect dramatic differences between
swimming speeds of athletes with only slightly different thrust.
However, the depth dependence is primarily due to
ventilation drag and/or wave drag,
as shown in Fig. 3.22 on p. 95.
The swimmer (even underwater) creates a wave that travels with her,
and must push along the "hump of water" that results;
the size of this "hump" decreases as she gets further from the surface.
Once she is far enough below the surface that we can ignore this effect,
we should be able to use Boye's formula on p. 93 for the hydrodynamic drag:
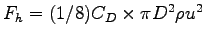 with
with
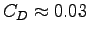 .
This gives
.
This gives
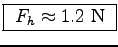 at u3 = 1.066 m/s.
at u3 = 1.066 m/s.
- Since the heart rate is about the same at all depths
one can assume that the propulsion force too is the same at all depths.
Calculate the drag coefficient ratio
CDy/CD3 as function of depth y.
ANSWER:
In unaccelerated motion at constant velocity, the propulsion force
is exactly balanced by the equal and opposite drag force,
so if one is constant, so is the other.
Since
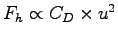 (everything else is constant),
a constant Fh implies
(everything else is constant),
a constant Fh implies
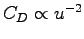 or
or
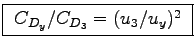 .
This can be used to calculate the ratio as a function of y.
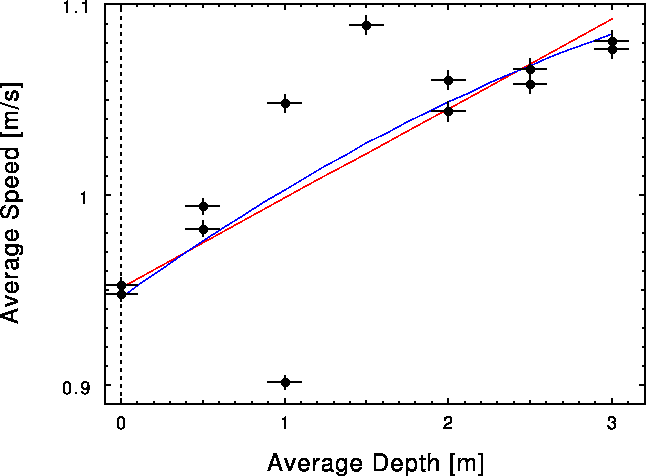
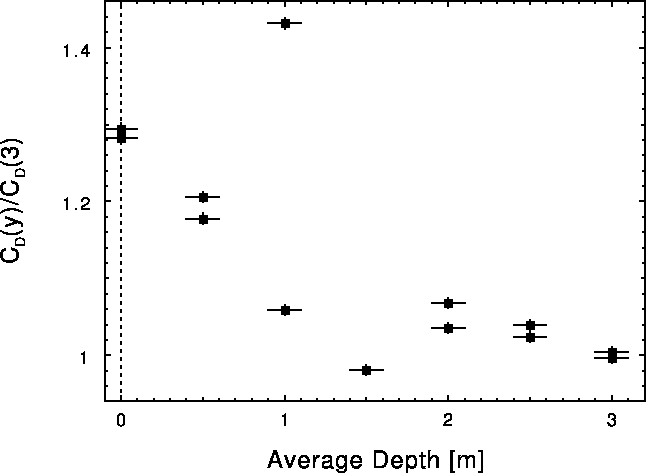
See the table and graph above.
Note however that the data "jump around" a lot,
indicating large systematic uncertainties (hardly surprising)
so we would be foolish to take the simple linear
or second order polynomial fits too seriously.
All we can really conclude is that "deeper tends to be better"
from the standpoint of the drag coefficient,
and possibly that the improvement levels off
after the first meter or two.
.
This can be used to calculate the ratio as a function of y.
See the table and graph above.
Note however that the data "jump around" a lot,
indicating large systematic uncertainties (hardly surprising)
so we would be foolish to take the simple linear
or second order polynomial fits too seriously.
All we can really conclude is that "deeper tends to be better"
from the standpoint of the drag coefficient,
and possibly that the improvement levels off
after the first meter or two.
- What advice should the UBC coach give to the swimmers?
ANSWER:
(i) Be grateful you're in a sport for which UBC provides a facility -
as opposed to (for instance) Track & Field, for which
UBC alone,
among all the major Universities in the civilised world,
has no facility (track) whatsoever!
(ii) On the start, always swim underwater
for as far and as deep as rules allow.
(There are strict limits on this, for obvious reasons.)
(iii) Natasha may decrease her lap time by swimming at a greater depth,
but of course she must return to the surface to breathe.
There is also another reason to stay at the surface:
air is thinner than water!
A swimmer may try to propel herself not only forward,
but also upward, so that her shoulders are only partly in the water,
thereby reducing the frontal area pushing against the water
and therewith the drag force.2
In addition, the wave itself may be utilized to a certain extent,
especially with butterfly and breast strokes.
If you observe competitive swimmers you will always see
an upward and downward oscillation,
which is partly used to overcome the wave,
especialy in the butterfly.
Surface waves aren't bad for everyone. The largest whales may be able to harness the energy from waves for their own propulsion3and dolphins are able to save energy by riding waves.4
Humans are not as well-streamlined as marine mammals: the drag coefficient for a towed human is nearly 3.5 times greater than a towed harbor seal.5
- Calculate the average speed of your fingers.
ANSWER:
Assuming that you hold your shoulder fixed and are flexible enough
to swing your arm in a circle, you can use
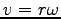 with r = L and
with r = L and
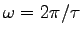 to calculate v.
For a typical L = 0.8 m and
to calculate v.
For a typical L = 0.8 m and 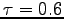 s this would give
v = 8.4 m/s.
s this would give
v = 8.4 m/s.
- Determine the radial centrifugal acceleration
and the additional pressure in the blood vessels
in your fingers due to the motion.
Compare this pressure to the systolic pressure
generated by your heart
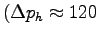 mm Hg),
and comment why your fingers are red.
ANSWER:
The radial acceleration of your fingers is given by
mm Hg),
and comment why your fingers are red.
ANSWER:
The radial acceleration of your fingers is given by
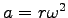 or a = v2/r.
For the typical values above, this would give a = 88 m/s2.
Compare the acceleration of gravity, g = 9.81 m/s2;
it is as if your arm were hanging down in a gravitational gradient
that starts at zero (at your shoulder) and increases linearly
to 8.9 g at your fingers.
Because the "artificial gravity" is not constant,
you can't just multiply
or a = v2/r.
For the typical values above, this would give a = 88 m/s2.
Compare the acceleration of gravity, g = 9.81 m/s2;
it is as if your arm were hanging down in a gravitational gradient
that starts at zero (at your shoulder) and increases linearly
to 8.9 g at your fingers.
Because the "artificial gravity" is not constant,
you can't just multiply 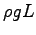 by 8.9 to get
the addidtional hydrostatic pressure at your fingers;
you must use the average a
(which, because a changes linearly with r,
is just half the value at your fingers)
or take the integral of
by 8.9 to get
the addidtional hydrostatic pressure at your fingers;
you must use the average a
(which, because a changes linearly with r,
is just half the value at your fingers)
or take the integral of 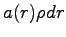 ,
which amounts to the same thing.
The result (for the above typical values) is p = 35,000 N/m2,
or about 1/3 of an atmosphere, or over
,
which amounts to the same thing.
The result (for the above typical values) is p = 35,000 N/m2,
or about 1/3 of an atmosphere, or over 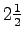 times the
typical systolic blood pressure of 13,300 Pa.
No wonder your fingers are red!
If the same blood pressure were produced in your head
for any length of time, you would be in grave danger of
an aneurysm or stroke. Fortunately the blood vessels in your
extremities were designed to handle such extremes.
times the
typical systolic blood pressure of 13,300 Pa.
No wonder your fingers are red!
If the same blood pressure were produced in your head
for any length of time, you would be in grave danger of
an aneurysm or stroke. Fortunately the blood vessels in your
extremities were designed to handle such extremes.
- What is the takeoff velocity?
ANSWER:
First let's assume that air drag is negligible,
in which case the initial kinetic energy
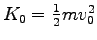 must equal the gravitational potential energy m g h
at the top of the (presumed vertical) trajectory,
i.e.
must equal the gravitational potential energy m g h
at the top of the (presumed vertical) trajectory,
i.e.
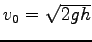 or
or
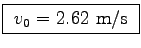 .
Now let's check to see if it is reasonable to neglect drag.
The Reynolds number of a sphere of D = 10-3 m
moving at u = 2.62 m/s through a medium with kinematic viscosity
.
Now let's check to see if it is reasonable to neglect drag.
The Reynolds number of a sphere of D = 10-3 m
moving at u = 2.62 m/s through a medium with kinematic viscosity
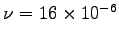 m2/s is
m2/s is
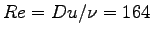 so the flow of air past the flea is laminar throughout and the
Stokes friction force is
so the flow of air past the flea is laminar throughout and the
Stokes friction force is
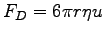 , where
, where
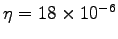 kg
kg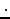 s
s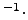 m-1
is the viscosity of air and
r = 0.5 x 10-3 m,
giving
FD = 0.44 x 10-6 N initially.
Thus the deceleration due to air friction
is af = FD/m where
m-1
is the viscosity of air and
r = 0.5 x 10-3 m,
giving
FD = 0.44 x 10-6 N initially.
Thus the deceleration due to air friction
is af = FD/m where
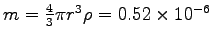 kg,
or af = 0.85 m/s2 - about 0.087 g.
This additional deceleration is a small fraction of
the deceleration due to gravity, and only gets smaller
as u decreases, so it is not a bad approximation
to neglect air friction - certainly our calculated v0
is off by less than 10%.
kg,
or af = 0.85 m/s2 - about 0.087 g.
This additional deceleration is a small fraction of
the deceleration due to gravity, and only gets smaller
as u decreases, so it is not a bad approximation
to neglect air friction - certainly our calculated v0
is off by less than 10%.
- How long is the acceleration phase?
ANSWER:
Assuming a constant acceleration of a0 = 2000 m/s2,
v0 = a0 t0 gives
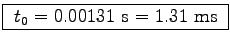 .
.
- What force is required to obtain this acceleration?
ANSWER:
We calculated
m = 0.52 x 10-6 kg earlier;
thus F0 = m a0 gives
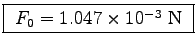 .
.
- What is the power (force x velocity) at takeoff?
ANSWER:
Since (assuming constant acceleration)
the velocity is initially zero and grows linearly with time
to a final value of v0, the power is initially zero and
grows linearly with time to a final value of F0 v0.
The average power is thus half the final power,
or
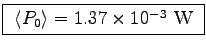 .
.
- Make a reasonable assumption about
the muscle mass involved in a jump
and calculate the power requirement per kg of muscle.
Given that a typical muscle output is
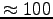 W/kg,
comment on your answer.
ANSWER:
Let's be generous and assume 1/5 of the entire mass of the flea
is muscle used in the jump. That would be about 10-7 kg.
The power-to-mass ratio would then be
W/kg,
comment on your answer.
ANSWER:
Let's be generous and assume 1/5 of the entire mass of the flea
is muscle used in the jump. That would be about 10-7 kg.
The power-to-mass ratio would then be
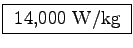 .
Even if the flea were all muscle, we would get
2620 W/kg, which is a little implausible!
There must be something else going on.
Oh yes . . .
.
Even if the flea were all muscle, we would get
2620 W/kg, which is a little implausible!
There must be something else going on.
Oh yes . . .
- Before a jump, the flea stores energy in a pad of resilin,
a rubber-like protein built into each hind leg,
about 30
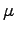 m thick and 80
m thick and 80 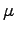 m in diameter,
with an energy storage capacity of about
1.5 x 106 J/m3.
How much potential energy could the flea store in each pad?
How long would it take the flea to put that much energy into each pad?
ANSWER:
The volume of a disc 30
m in diameter,
with an energy storage capacity of about
1.5 x 106 J/m3.
How much potential energy could the flea store in each pad?
How long would it take the flea to put that much energy into each pad?
ANSWER:
The volume of a disc 30 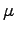 m thick and 80
m thick and 80 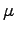 m in diameter is
0.151 x 10-12 m3, so it could store
m in diameter is
0.151 x 10-12 m3, so it could store
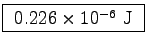 .
Assuming that the "mouse to elephant" allometric relation
holds, the flea's resting metabolism is about
.
Assuming that the "mouse to elephant" allometric relation
holds, the flea's resting metabolism is about
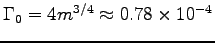 W.
If the flea stores energy in its resilin pads at roughly this rate,
it will take about
W.
If the flea stores energy in its resilin pads at roughly this rate,
it will take about
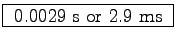 for the flea to store up enough energy for another jump.
(Presumably it will eventually get tired if it keeps this up,
but it can obviously jump pretty often!)
for the flea to store up enough energy for another jump.
(Presumably it will eventually get tired if it keeps this up,
but it can obviously jump pretty often!)