- Search the literature to collect data about a fast hunter
such as wild dog, leopard, or lion.1 Find mass M, top speed Ut, length of leg L,
length of step while foot is on the ground S,
period
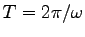 (either from T = 1/n
where n is the number of steps per second,
or from the distance
(either from T = 1/n
where n is the number of steps per second,
or from the distance 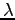 between
two imprints of the feet on the ground:
between
two imprints of the feet on the ground:
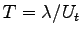 ,
duration
,
duration 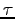 of the hunt, or the range
of the hunt, or the range 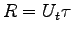 .
Treat the motion of the rear leg like simple harmonic motion
where the position of the foot relative to the vertical is
.
Treat the motion of the rear leg like simple harmonic motion
where the position of the foot relative to the vertical is
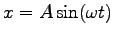 , where A = S/2 is the amplitude,
and
, where A = S/2 is the amplitude,
and
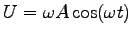 is the velocity of the foot.
The maximum foot velocity is
is the velocity of the foot.
The maximum foot velocity is
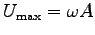 ,
the instantaneous acceleration of the foot is
,
the instantaneous acceleration of the foot is
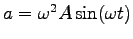 ,
and the maximum foot acceleration is
,
and the maximum foot acceleration is
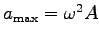 .
ANSWER:
.
ANSWER:
Body mass: M = 40 kg (Marker and Dickman, 2003).3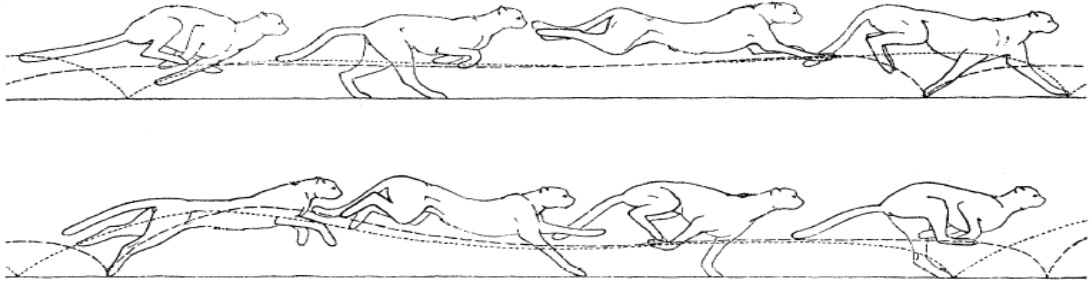
Cheetah, Acinonyx jubatus. (Fig. from Hildebrand, 1962)2
Average top speed: Ut = 14.8 m/s (Hildebrand, 1962).
Limb Length: L = 0.79 m (Marker and Dickman, 2003).
Average period: T = 0.31 s (Hildebrand, 1962).
Angular deflection of the limb: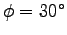 (Ahlborn, 2004).
(Ahlborn, 2004).
Distance covered during hunt: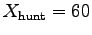 m.
m.
Duration of hunt: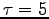 s.
s.
The parameters that control the speed U are stride length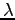 and stride frequency f (Alexander, 2003):4
and stride frequency f (Alexander, 2003):4
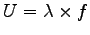 .
Therefore, we can calculate a stride length for a given speed
and stride frequency:
f = 1/T = 1/0.31 s = 3.3 Hz and (at top speed)
.
Therefore, we can calculate a stride length for a given speed
and stride frequency:
f = 1/T = 1/0.31 s = 3.3 Hz and (at top speed)
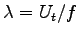 = (14.8 m/s)/(3.3 Hz)
or
= (14.8 m/s)/(3.3 Hz)
or
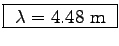 .
.
To get the length S of a "step" requires some knowledge of the leg motion. If we treat this as the swing of a straight rod of length L through an arc subtending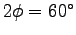 at constant
at constant  (ignoring the fact that this would be a pretty bumpy ride),
we can set
(ignoring the fact that this would be a pretty bumpy ride),
we can set 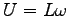 and pretend that the leg just keeps
swinging around in a circle at the same
and pretend that the leg just keeps
swinging around in a circle at the same 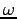 (like in a "Roadrunner" cartoon),
in which case the step length S is
the same fraction of the total stride length
(like in a "Roadrunner" cartoon),
in which case the step length S is
the same fraction of the total stride length  as
as 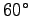 is of
is of 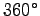 - namely 1/6.
This immediately gives (at top speed) a step length
- namely 1/6.
This immediately gives (at top speed) a step length 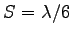 or
or
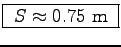 .
Alternatively, we can ignore the details of
how the leg might bend during the step
and simply assume that it begins with
the leg stretched out straight at a
.
Alternatively, we can ignore the details of
how the leg might bend during the step
and simply assume that it begins with
the leg stretched out straight at a 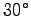 angle in front
(so that the shoulder is
angle in front
(so that the shoulder is
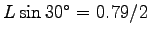 m behind the foot
at the moment the foot first touches the ground)
and ends with the leg stretched out straight
at the same angle behind the shoulder
(so that the shoulder is 0.79/2 m ahead of the foot
as it leaves the ground) for a total step length of
m behind the foot
at the moment the foot first touches the ground)
and ends with the leg stretched out straight
at the same angle behind the shoulder
(so that the shoulder is 0.79/2 m ahead of the foot
as it leaves the ground) for a total step length of
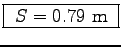 , consistent with the estimate above.
, consistent with the estimate above.
- Assuming that the maximum acceleration of the foot
is equal to the maximum acceleration of the body, find
the acceleration time t1 needed to reach top speed Ut = a t1.
ANSWER:
The maximum acceleration of the foot
(in the context of simple harmonic motion) is
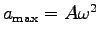 where A is the amplitude,
where A is the amplitude,
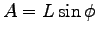 = (0.79 m
= (0.79 m
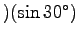
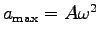 = (0.79 m)(3.3 Hz)2 = 8.6 m/s2.
Of course, this maximum horizontal acceleration
occurs at the end of the range of motion
(e.g., for the "Road Runner" picture, when the leg is horizontal)
and at mid-stride the horizontal acceleration in this model would be zero;
so we are bound to be overestimating the maximum acceleration
by something like a factor of two.
The problem tells us to assume that the acceleration of the foot
is equal to the acceleration of the body,
= (0.79 m)(3.3 Hz)2 = 8.6 m/s2.
Of course, this maximum horizontal acceleration
occurs at the end of the range of motion
(e.g., for the "Road Runner" picture, when the leg is horizontal)
and at mid-stride the horizontal acceleration in this model would be zero;
so we are bound to be overestimating the maximum acceleration
by something like a factor of two.
The problem tells us to assume that the acceleration of the foot
is equal to the acceleration of the body,
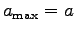 , so the time to reach top speed is
t1 = Ut/a = (14.8 m/s)/(8.6 m/s2)
or
, so the time to reach top speed is
t1 = Ut/a = (14.8 m/s)/(8.6 m/s2)
or
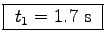 .5
.5
- Determine the speed-up distance s1
(similar to the free fall distance
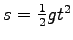 ).
ANSWER:
The speed-up distance is similar to free fall distance,
but instead of gravity we use our calculated acceleration:
).
ANSWER:
The speed-up distance is similar to free fall distance,
but instead of gravity we use our calculated acceleration:
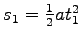 = (0.5)(8.6 m/s2)(1.7 s)2
or
= (0.5)(8.6 m/s2)(1.7 s)2
or
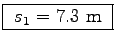 .
.
- Calculate the kinetic energy K
which the animal attains at top speed.
ANSWER:
This is straightforward:
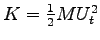 = (0.5)(40 kg)(14.8 m/s)2 or
= (0.5)(40 kg)(14.8 m/s)2 or
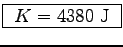 .6
.6
- Assuming that K was obtained by the application of
an average force F acting during the time t1
or over the distance s1,
the energy equation reads
K = F x s1,
from which F can be found.
ANSWER:
Given K = 4380 J and s1 = 7.3 m, we use F = K/s1
to get
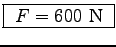 .
.
- Find the total energy expense of the hunt,
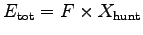 and express it in mass of body fat burned,
taking into account a reasonable inefficiency of
converting the body fat into muscle fuel.7 ANSWER:
and express it in mass of body fat burned,
taking into account a reasonable inefficiency of
converting the body fat into muscle fuel.7 ANSWER:
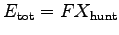 = (600 N)(60 m)
or
= (600 N)(60 m)
or
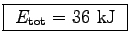 .
Such a short sprint would not normally be reflected in
the conversion of fat to fuel, but rather
governed by anærobic metabolic pathways.
The muscle biochemistry and histology of cheetah locmotor muscles
show a high capacity for glycolysis and indicate that they are
well equipped for anærobic metabolism.8Nevertheless, the energy has to eventually come from some form of
"chemical fuel", and if the cheetah had no other source
than its own body fat, it would have to "burn" a mass
.
Such a short sprint would not normally be reflected in
the conversion of fat to fuel, but rather
governed by anærobic metabolic pathways.
The muscle biochemistry and histology of cheetah locmotor muscles
show a high capacity for glycolysis and indicate that they are
well equipped for anærobic metabolism.8Nevertheless, the energy has to eventually come from some form of
"chemical fuel", and if the cheetah had no other source
than its own body fat, it would have to "burn" a mass
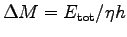 where
where
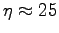 %
is the efficiency of utilization for work and
h = 32 x 106 J/kg is the specific energy content of fat.
This gives
%
is the efficiency of utilization for work and
h = 32 x 106 J/kg is the specific energy content of fat.
This gives
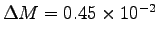 kg
or
kg
or
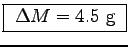 .
(The cheetah needs to be successful at least once
in every few hundred tries or she will get pretty skinny!)
.
(The cheetah needs to be successful at least once
in every few hundred tries or she will get pretty skinny!)
- Determine the impact speed U0.
ANSWER:
You can use either the constant acceleration equation U02 = 2 g h
or the conservation of energy
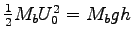 to get
to get
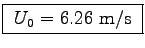 .
.
- Calculate the deceleration (negative acceleration)
of the the boy's center of mass during landing,
and determine the average force
on the soles of his shoes during impact.
ANSWER:
We have little choice but to assume the mud exerts a constant force
Fb during the boy's impact, absorbing his entire kinetic energy
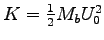 as work
as work
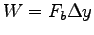 done on the mud.
Thus
done on the mud.
Thus
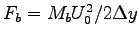 = (70 kg)(6.26 m/s
)2/(2 x 0.05 m)
or
= (70 kg)(6.26 m/s
)2/(2 x 0.05 m)
or
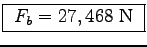 or 40 times his weight.
Ouch!
or 40 times his weight.
Ouch!
- The girl (Mg = 65 kg) lands on the rock,
but in order to reduce the impact force she lands with soft knees
and moves her center of gravity relative to her feet
by
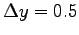 m as she lands.
What is the average impact force
on the soles of her feet during the landing?
ANSWER:
The velocity on impact U0 is the same for both.
For the young woman we use the same equation,
except that
m as she lands.
What is the average impact force
on the soles of her feet during the landing?
ANSWER:
The velocity on impact U0 is the same for both.
For the young woman we use the same equation,
except that 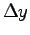 is 10 times bigger
and her mass Mg is less,
so the average force is more than ten times smaller:
is 10 times bigger
and her mass Mg is less,
so the average force is more than ten times smaller:
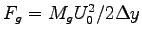 = (65 kg)(6.26 m/s
)2/(2 x 0.5 m)
or
= (65 kg)(6.26 m/s
)2/(2 x 0.5 m)
or
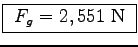 or 4 times her weight.
or 4 times her weight.
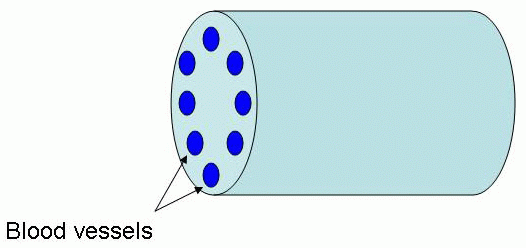
- Determine the surface area A of the gills
that contributes to the diffusion exchange of oxygen.
ANSWER:
Mass of nudibranch: M = 0.005 kg.
Mass of gills: m = 0.0005 kg.
Gill volume Vg = (0.0005 kg)/(1000 kg/m3)
= 5 x 10-7 m3.
Gill `trunk' diameter
dg = 500 x 10-6 m.
Gill capillary diameter
dc = 10 x 10-6 m.
If we treat the entire gill volume as one long cylinder
of diameter dg, its length Lg can be deduced from
its volume
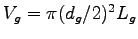 :
:
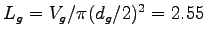 m.
Then we can calculate its surface area as
m.
Then we can calculate its surface area as
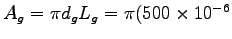 m)(2.55 m)
or
m)(2.55 m)
or
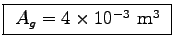 .
.
- Calculate the diffusion flow rate of oxygen
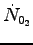 [molecules/sec] into the gills.
(See Sect. 4.1.3; assume first that
the blood returning from the body into the gills
is completely deoxygenated.)
ANSWER:
The diffusion flux
[molecules/sec] into the gills.
(See Sect. 4.1.3; assume first that
the blood returning from the body into the gills
is completely deoxygenated.)
ANSWER:
The diffusion flux
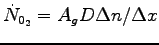 ,
Where Ag is the area over which diffusion occurs,
D is the diffusion coefficient and
,
Where Ag is the area over which diffusion occurs,
D is the diffusion coefficient and
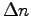 is the change in concentration
over a given distance
is the change in concentration
over a given distance 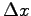 .
.
Here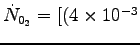 m
2)
(18 x 10-10 m2/s
)
(1.63 x 1023 molecules O2/m3 H2O
)]
/(10 x 10-6 m) or
m
2)
(18 x 10-10 m2/s
)
(1.63 x 1023 molecules O2/m3 H2O
)]
/(10 x 10-6 m) or
 .
.
- Use the relation between
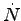 and
and 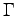 which is derived in Section 4.3.3
to determine the metabolic rate of the nudibranch.
ANSWER:
which is derived in Section 4.3.3
to determine the metabolic rate of the nudibranch.
ANSWER:
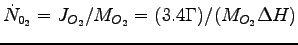 .
.
Thus 1.17 x 1017 molecules O2/s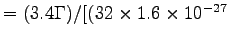 kg)(30 MJ/kg)]
kg)(30 MJ/kg)]
so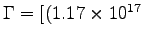 molecules O2/s
)
(32 x 1.6 x 10-27 kg)(30 MJ/kg)]/3.4
= 5.3 x 10-8 MJ/s
or
molecules O2/s
)
(32 x 1.6 x 10-27 kg)(30 MJ/kg)]/3.4
= 5.3 x 10-8 MJ/s
or
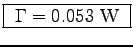 .
.
- Assuming that for these animals
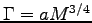 ,
determine the metabolic constant a.
ANSWER:
,
determine the metabolic constant a.
ANSWER:
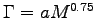
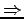
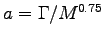 = 0.053/0.0050.75
or
= 0.053/0.0050.75
or
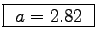 .
.
- Look into the literature to assess if the assumption is reasonable
that the blood returning from the body into the gills
is completely deoxygenated. If not, how would this change your answers?
ANSWER:
Many references show curves similar to those in Fig. 4.17 on p. 145
of the textbook, indicating that essentially all hæmoglobin
oxygen bonding sites are empty when in equilibrium with a reservoir
at zero partial pressure of O2.
However, living tissue is unlikely to have zero
partial O2 pressure at any time, so this is not too helpful.
The "Bohr effect" (see above) helps squeeze more O2 out of hæmoglobin sites by filling them with CO2 supplied by the same tissues, which helps but does not really answer the question. Figure 4.18(b) on p. 146 suggests that the equilibrium O2 partial pressure in venous blood returning to the lungs is about 5 kPa, compared with about 12.5 kPa for oxygenated blood leaving the lungs, which means that venous blood is still about 40% oxygenated. Since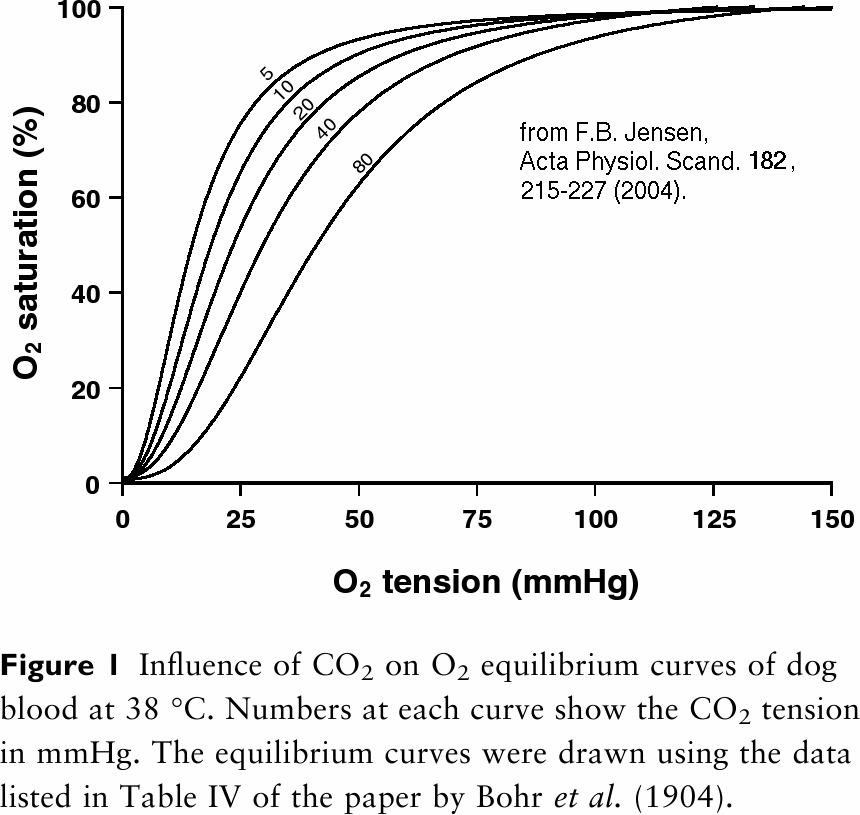
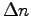 is the O2 concentration difference between
the water (which we assume has the same O2 partial pressure as air,
namely about 20 kPa) and the deoxygenated blood, if the latter has
is the O2 concentration difference between
the water (which we assume has the same O2 partial pressure as air,
namely about 20 kPa) and the deoxygenated blood, if the latter has
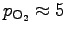 kPa instead of zero as assumed above, it will
reduce
kPa instead of zero as assumed above, it will
reduce
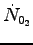 by a factor of 15/20 = 0.75,
and the other calculations should be adjusted accordingly.
by a factor of 15/20 = 0.75,
and the other calculations should be adjusted accordingly.