- BA's right eye was producing blurred images because
the lens was getting "cloudy" and scattering some light.
A cataract operation was performed where the natural lens
was replaced by an artificial lens . . . .
The natural lens had n = 1.413 and radii of curvature r1 = 10 mm and r2 = 7.8 mm when focused at infinity. What was its focal length? ANSWER: There is some ambiguity to the question, inasmuch as the focal length of a lens depends upon the index of refraction of the medium in which it is immersed (see p. 273 of the textbook). However, when "the focal length" is discussed without reference to any medium, it is conventional to assume that the medium is vacuum or air with no = ni = 1. In that case we can use the simple thin lens approximation
so that in this case the "optical power" is 1/f = 0.09425 mm-1 and the focal length is f = 10.61 mm. But the LENSMAKER'S EQUATION says
where d is the thickness of the lens along its central axis. Assuming the lens is about 5 mm in diameter, a quick sketch shows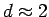 mm, in which case the extra term in Eq. (2)
reduces the optical power by about 0.003 mm-1
or a little over 3%; the true f is thus about 3% longer, or
mm, in which case the extra term in Eq. (2)
reduces the optical power by about 0.003 mm-1
or a little over 3%; the true f is thus about 3% longer, or
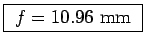 .
.
- It was replaced by an artificial symmetric lens with
r = r1 = r2 made from crown glass (n = 1.52),
what radius r gives the same focal length as before?
ANSWER:
First let's see what radius we get from Eq. (1):
1/10.96 = (1.52-1)[2/r]
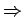 r = 10.96 x 0.52 x 2
or
r = 10.96 x 0.52 x 2
or
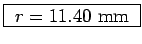 .
Another sketch suggests that this would make d even smaller.
We could iterate the calculation with Eq. (2)
to get a better approximation,
but the result will certainly be within 2% of the above value.
.
Another sketch suggests that this would make d even smaller.
We could iterate the calculation with Eq. (2)
to get a better approximation,
but the result will certainly be within 2% of the above value.
- What should be the radius of curvature
if the lens were made from silicate flint glass
with n = 1.65?
ANSWER:
The same arithmetic with the new n gives
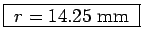 .
.
with no = 1 and ni = 1.336 to get 1.336/i1 = 1/fc - 1/o1 = 0.0431 - 1/250 = 0.0391 or
This image serves as the (virtual) object
(object distance o2 = -i1)
from which the eye lens creates a real image I2
on the retina at the image distance i2 = 20 mm.
The eye lens must contract to create a sharp image
of such a close-distance object.
Find the radius of curvature of the eye lens
when focused at the object,
assuming that the lens contracts symmetrically
so that
r250 = r1 = r2.
ANSWER:
We use Eq. (3) again to solve for the required
focal length of the lens:
1/f = no/o2 + ni/i2
= -1.336/34.19 + 1.336/20 = 0.0277 mm-1 or f = 36.07 mm.
We must now modify Eq. (1)
to account for the index of the medium:
- How many facet eyes are there in each compound eye
if the cones touch each other?
ANSWER:
The total area of the hemispherical surface is
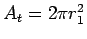 = 2.51 x 10-5 m2.
The area of one cone top is
= 2.51 x 10-5 m2.
The area of one cone top is
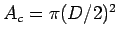 = 0.785 x 10-8 m2.
We can't just divide At by Ac because the facets
are explicitly assumed to be circular, and a close-packed
array of identical circles does not fill the entire area;
there is a little "dead space" left over.
If the array were square, the "filling factor" would be
just
= 0.785 x 10-8 m2.
We can't just divide At by Ac because the facets
are explicitly assumed to be circular, and a close-packed
array of identical circles does not fill the entire area;
there is a little "dead space" left over.
If the array were square, the "filling factor" would be
just 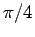 (the ratio of a circle's area to that of a square
with one side equal to the diameter of the circle);
but the array is hexagonal, as can be seen from
Fig. 8.24(b) on p. 293 of the textbook.
In this case the filling factor is 90.69%,
so the number of facets should be
N = 0.9069 At/Ac
or
(the ratio of a circle's area to that of a square
with one side equal to the diameter of the circle);
but the array is hexagonal, as can be seen from
Fig. 8.24(b) on p. 293 of the textbook.
In this case the filling factor is 90.69%,
so the number of facets should be
N = 0.9069 At/Ac
or
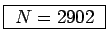 .
.
- What is the critical angle
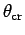 of total internal reflection in the light pipe?
ANSWER:
In general
of total internal reflection in the light pipe?
ANSWER:
In general
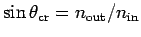 .
In this case
.
In this case
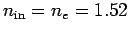 and
and
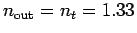 ,
giving
,
giving
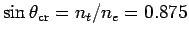 and
and
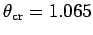 radians or (in silly conventional units)
radians or (in silly conventional units)
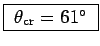 .
.
- What is the acceptance angle
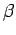 for the light pipe section by itself [see Fig. 8.23(b)]?
ANSWER:
Referring to Fig. 8.23 and following the instructions
at the bottom of p. 291,
we first convert
for the light pipe section by itself [see Fig. 8.23(b)]?
ANSWER:
Referring to Fig. 8.23 and following the instructions
at the bottom of p. 291,
we first convert
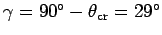 into
into 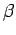 using Snell's Law,
using Snell's Law,
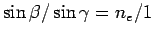 or
or
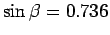 giving
giving
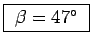 .
.
- What is the cone angle
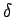 ?
ANSWER:
From simple geometry,
?
ANSWER:
From simple geometry,
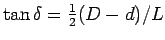 = 0.5 x 50 x 10-6/200 x 10-6
= 0.125 giving
= 0.5 x 50 x 10-6/200 x 10-6
= 0.125 giving
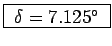 .
.
- Explain qualitatively why the acceptance angle
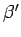 for light pipe and cone [see Fig. 8.23(c)] is smaller than
for light pipe and cone [see Fig. 8.23(c)] is smaller than 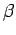 .
ANSWER:
Without the lens focusing the light into the cone
as in Fig. 8.24(a), a ray entering the front of the cone
at an angle
.
ANSWER:
Without the lens focusing the light into the cone
as in Fig. 8.24(a), a ray entering the front of the cone
at an angle 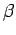 will reach the inner surface of the cone
at an angle of
will reach the inner surface of the cone
at an angle of
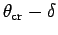 , which is too small
for total internal reflection and will thus be lost.
Only if the incoming angle is
, which is too small
for total internal reflection and will thus be lost.
Only if the incoming angle is
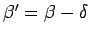 or less
will TIR be achieved in the cone section.
or less
will TIR be achieved in the cone section.
- Name 5 other animals that have compound eyes.
ANSWER:
Trilobites, spiders, crabs, shrimp and any other arthropods.
- Find and sketch 3 examples of optical illusions.
Explain how the eye has been deceived in each case.
ANSWER:
There are thousands of examples; this was meant to be fun!
- Describe one example of an optical trick used by an animal
to hide from or scare off its predators.
ANSWER:
Again, there are many examples: an animal may disguise itself as
a leaf, stick or rock, if it is about the right size;
it may look like another animal that is venomous
or distasteful. The possibilities are endless.
- Describe an example of an animal that appears colorful
due to either interference or diffraction,
and explain in words what the "optical components" do
to the light waves to generate the colors.
ANSWER:
Once again there are many examples, but of course our favourite is
the blue (on one side) butterfly:
which achieves its brilliant colour by thin film interference in which the scales on its wings have a thickness just right for constructive interference between blue light reflected off both sides of the transparent scales and destructive interference between red light reflected off both sides.

![\begin{displaymath}
{1 \over f} = (n-1)\left[ {1 \over r_1} + {1 \over r_2} \right]
\end{displaymath}](img1.gif)
![\begin{displaymath}
{1 \over f} = (n-1)\left[ {1 \over r_1} + {1 \over r_2}
- {(n-1) d \over n r_1 r_2 } \right]
\end{displaymath}](img2.gif)
![\begin{displaymath}
{1 \over f} = \left[ {(n_g - n_o) \over r_1}
+ {(n_g - n_i) \over r_2} \right]
\end{displaymath}](img11.gif)