

Next: Monotonic-decreasing field-magnitude distributions
Up: Uemura's Site-Distribution Trick
Previous: (Gaussian)x(power) distribution of Gaussians
As an example of a case where a field-magnitude distribution with no peak at
finite 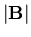 is generated by this kind of convolution, let
is generated by this kind of convolution, let
be convoluted with a Lorentzian distribution at each site:
In spite of these expressions not being well defined when Bi=w or B=w,
these distributions are smooth through those values.
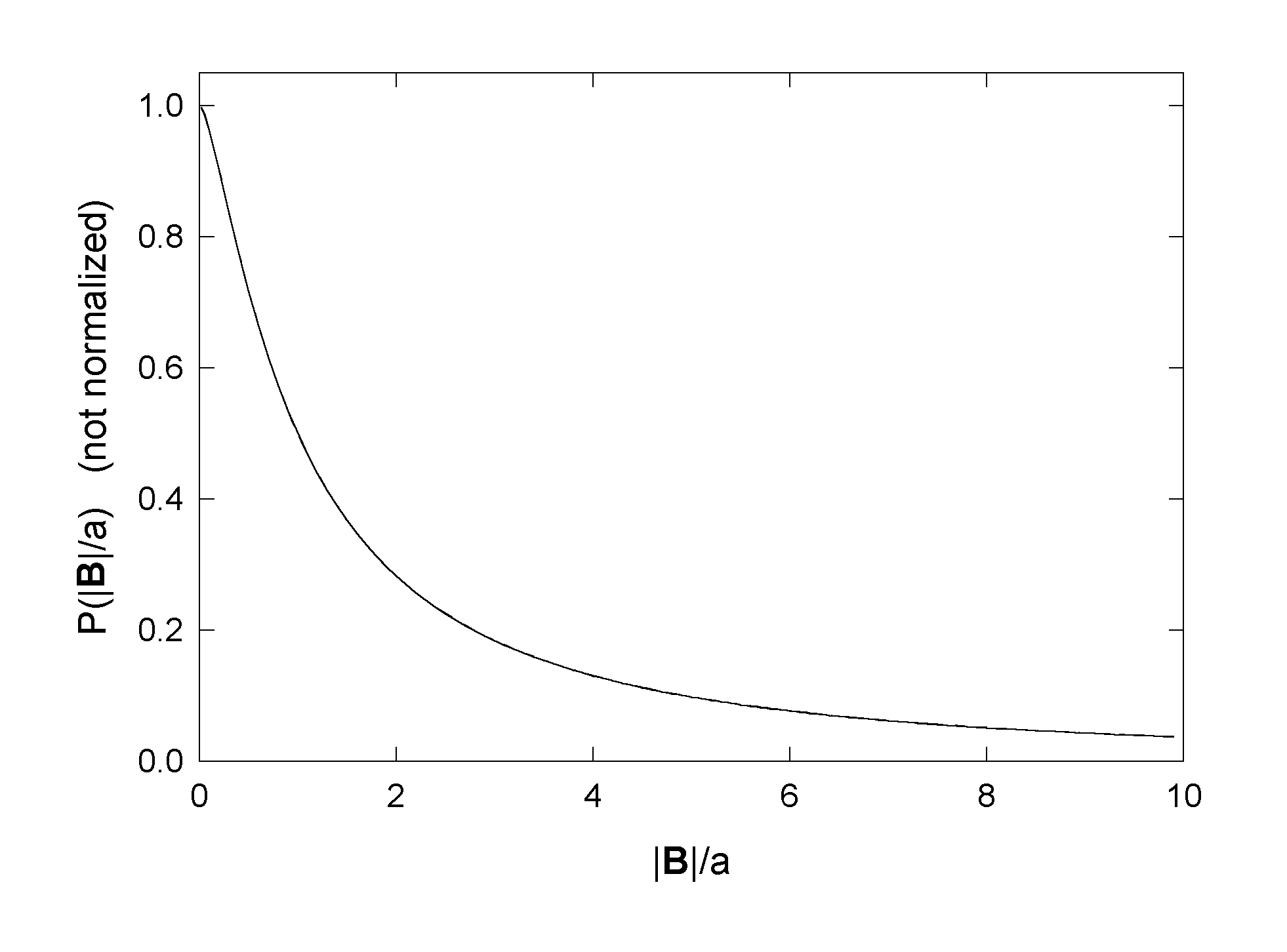
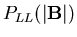 is
shown in Fig.5. Note that it is finite, nonzero at B=0. The corresponding
relaxation function is expressible in sine-integral and cosine-integral
functions.
is
shown in Fig.5. Note that it is finite, nonzero at B=0. The corresponding
relaxation function is expressible in sine-integral and cosine-integral
functions.
Figure 5:
Jess H. Brewer
2002-09-24
![\begin{displaymath}\begin{array}{c}
P_{LL}(B_i)= \frac{(norm)\ln \left( \frac{B . . .
. . . t( \frac{B^2}{\textrm{w}^2}-1\right)
}\right] .
\end{array}
\end{displaymath}](img46.gif)
