Science 1 Physics
Exercise 1 (14 Sep 2009) SOLUTIONS
(Not to be turned in)
Note:
I will occasionally insert errors in the solutions
just to see if you are paying attention. This is always
intentional, because, as you know, Professors never
make mistakes! I offer a $2 prize for the first person to
notice such a mistake and notify me by Email.
(Detection of such intentional errors in class is only worth $1,
because I like to sprinkle in more of them there.
:-)
-- Jess
"Waves I "
Work through problems 44, 54, 66, 72 and 76
from Knight, Ch. 20.
44: A wave travels along a string at a speed of 280~m/s.
What will be the speed if the string is replaced by one made of
the same material and under the same tension
but having twice the radius?
Twice the radius implies four times the cross-sectional area,
so the linear density of the new string is four times that of
the original string. Since the propagation speed of a wave
in a stretched string is equal to the square root of the ratio of
the tension to the linear density, the new propagation speed
is one half of the old one.
54: A wave on a string is described by
D(x,t) =
(2.00 cm)*sin[(12.57 rad/m)*x - (638 rad/s)*t],
where x is in m and t is in s.
The linear density of the string is 5.00 g/m. What are
(a) the string tension?
(b) the maximum displacement of a point on the string?
(c) the maximum speed of a point on the string?
(a) One can read directly off the formula for D(x,t)
the amplitude Dmax = 2.00 cm = 0.02 m,
the wavenumber k = 12.57 rad/m,
the angular frequency 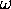 = 638 rad/s
and the initial phase (zero). Since the propagation speed
c =
= 638 rad/s
and the initial phase (zero). Since the propagation speed
c = 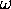 /k = 50.76 m/s
is the square root of the ratio of the tension T
to the linear density µ = 5.00 g/m = 0.005 kg/m,
we have 50.762 = 2576 = T/0.005 or
T = 12.88 N. (Note that we have to convert
everything to SI units if we want to use the general formulae.)
/k = 50.76 m/s
is the square root of the ratio of the tension T
to the linear density µ = 5.00 g/m = 0.005 kg/m,
we have 50.762 = 2576 = T/0.005 or
T = 12.88 N. (Note that we have to convert
everything to SI units if we want to use the general formulae.)
(b) Given: Dmax = 2.00 cm = 0.02 m.
(c) v = dD/dt = - 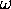 Dmax cos(kx -
Dmax cos(kx - 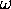 t),
which has its maximum value when the cosine function equals -1:
vmax =
t),
which has its maximum value when the cosine function equals -1:
vmax = 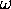 Dmax
= 638*0.02 = 12.76 m/s.
Dmax
= 638*0.02 = 12.76 m/s.
66: Lasers can be used to drill or cut material.
One such laser generates a series of high-intensity pulses
rather than a continuous beam of light.
Each pulse contains 500 mJ or energy and lasts 10 ns.
The laser fires 10 such pulses per second.
(a) What is the peak power of the laser light?
The peak power is the power during one of the 10 ns pulses.
(b) What is the average power output of the laser?
The average power is the total energy delivered per second.
(c) A lens focuses the laser beam to a
10-µm-diameter circle on the target.
During the pulse, what is the light intensity on the target?
(d) The intensity of sunlight at midday is
about 1100 W/m2.
What is the ratio of the laser intensity on the target
to the intensity of the midday sun?
(a) 500 mJ / 10 ns = 0.5 J / 10-9 s = 5*108 W.
(b) The laser is "on" for only 100 ns altogether every second,
which amounts to 10-7 of the time.
The average power is thus 10-7 of the power when it's on,
or 50 W.
(c) The spot has a radius of r = 5*10-6 m
so its area is 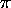 r2
= 0.785*10-10 m2. The intensity I is
the power per unit area, so I =
5*108/0.785*10-10 = 6.37*1018 W/m2.
r2
= 0.785*10-10 m2. The intensity I is
the power per unit area, so I =
5*108/0.785*10-10 = 6.37*1018 W/m2.
(d) The question does not specify whether you should calculate
the peak intensity I = 5.79*1015 Isun
or the average intensity, <I> =
5.79*108 Isun,
so we'll do both. Either way, it's pretty hot!
72: A physics professor demonstrates the Doppler effect
by tying a 600 Hz sound generator to a 1.0-m-long rope
and whirling it around her head in a horizontal circle
at 100 rpm. What are the highest and lowest frequencies
heard by a student in the classroom?
The frequency of sound from a moving source is shifted by a ratio
1/(1 - v/vs) where vs
is the speed of sound (typically 343 m/s) and v is the speed
of the source coming toward the observer. (This form also works
when the source is moving away; then v -s negative.)
So we need only calculate v = r 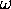 where r = 1 m and
where r = 1 m and 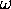 = 2
= 2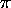
 = 2
= 2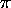 *100/60 = 10.5 s-1.
Thus v = 10.5 m/s, v/vs = 0.0305
and f = (600 Hz)/(1
*100/60 = 10.5 s-1.
Thus v = 10.5 m/s, v/vs = 0.0305
and f = (600 Hz)/(1  0.0305),
giving a lowest frequency of 582 Hz and a highest frequency
of 619 Hz.
0.0305),
giving a lowest frequency of 582 Hz and a highest frequency
of 619 Hz.
76: Wavelengths of light from a distant galaxy
are found to be 0.5% longer than the corresponding wavelengths
measured in a terrestrial laboratory.
Is the galaxy approaching or receding from the earth?
At what speed?
The wavelength gets longer ("red shift") if the galaxy is
receding from Earth, which is generally the case.
The square of the ratio of the observed wavelength
to the original wavelength of light emitted by a receding source
is given by (1 +  )/(1 -
)/(1 -  )
where
)
where  is the ratio of the receding speed
of the object to the speed of light.
Thus (1.005)2 = 1.010025
is the ratio of the receding speed
of the object to the speed of light.
Thus (1.005)2 = 1.010025
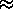 1.01 =
(1 +
1.01 =
(1 +  )/(1 -
)/(1 -  )
or (1 +
)
or (1 +  ) = 1.01 (1 -
) = 1.01 (1 -  )
or 2.01
)
or 2.01  = 0.01
or
= 0.01
or  = 0.01/2.1025 = 0.005
(note that we have kept extra significant figures during the calculation
but dropped back to one significant figure at the end).
Since the speed of light is (to this precision) 3*108 m/s,
we have v = 1.5*106 m/s.
A pretty good clip!
= 0.01/2.1025 = 0.005
(note that we have kept extra significant figures during the calculation
but dropped back to one significant figure at the end).
Since the speed of light is (to this precision) 3*108 m/s,
we have v = 1.5*106 m/s.
A pretty good clip!
Jess H. Brewer -
Last modified: Wed Sep 23 21:53:40 PDT 2009
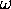 = 638 rad/s
and the initial phase (zero). Since the propagation speed
c =
= 638 rad/s
and the initial phase (zero). Since the propagation speed
c = 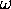 /k = 50.76 m/s
is the square root of the ratio of the tension T
to the linear density µ = 5.00 g/m = 0.005 kg/m,
we have 50.762 = 2576 = T/0.005 or
T = 12.88 N. (Note that we have to convert
everything to SI units if we want to use the general formulae.)
/k = 50.76 m/s
is the square root of the ratio of the tension T
to the linear density µ = 5.00 g/m = 0.005 kg/m,
we have 50.762 = 2576 = T/0.005 or
T = 12.88 N. (Note that we have to convert
everything to SI units if we want to use the general formulae.)
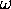 Dmax cos(kx -
Dmax cos(kx - 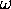 t),
which has its maximum value when the cosine function equals -1:
vmax =
t),
which has its maximum value when the cosine function equals -1:
vmax = 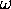 Dmax
= 638*0.02 = 12.76 m/s.
Dmax
= 638*0.02 = 12.76 m/s.
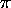 r2
= 0.785*10-10 m2. The intensity I is
the power per unit area, so I =
5*108/0.785*10-10 = 6.37*1018 W/m2.
r2
= 0.785*10-10 m2. The intensity I is
the power per unit area, so I =
5*108/0.785*10-10 = 6.37*1018 W/m2.
 = 2
= 2 0.0305),
giving a lowest frequency of 582 Hz and a highest frequency
of 619 Hz.
0.0305),
giving a lowest frequency of 582 Hz and a highest frequency
of 619 Hz.
 )/(1 -
)/(1 - 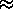 1.01 =
(1 +
1.01 =
(1 +