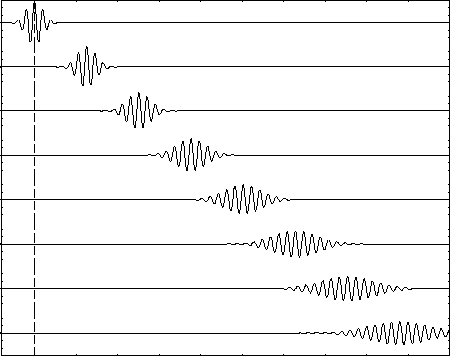
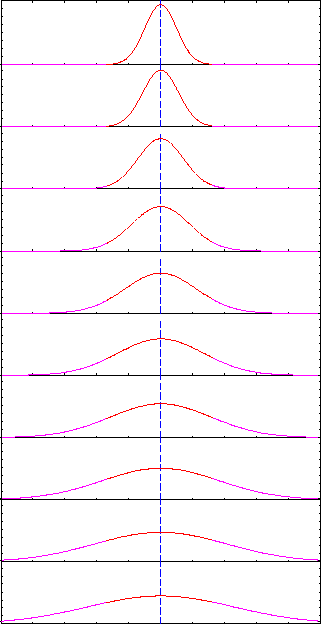
The centre of a wave packet with a finite ko
moves with time at the group velocity, as expected for
the mean position of a particle. It simultaneously broadens
just like the (on average) stationary particle; this must be so in order
to preserve Galilean invariance, which is still applicable as long as
the velocities are nonrelativistic.
This raises the question: What do the "wiggles" represent?
When the particle is (on average) at rest, its wave packet is just a
"bump" that spreads out with time; when it is moving, it acquires all
these oscillations of phase with a wavelength satisfying de Broglie's
formula. Is it really "there" at the peaks and "not there" at the
points where the function crosses the axis? No. Except for the
overall "envelope" it is just as "there" at one point as at another.
This is a direct consequence of using the complex exponential form
(rather than a cosine) for the travelling wave.
Although the plots above show only the real part,
there is an imaginary part that is a maximum when the real part is zero
and vice versa so that the absolute magnitude is always
(except for the overall "envelope") the same.
In that case, what is the point of even having these "wiggles?"
Well, although no experiment can measure the absolute phase
of a wavefunction, the relative phase of two probability
amplitudes being added together is what causes interference,
which is the key to all observable quantum mechanical phenomena.
It is also worth remembering that by adding together two travelling waves
propagating in opposite directions it is possible to make
a standing wave, whose wavefunction really is a real oscillatory
function for which the particle is actually never found at positions
where the amplitude is zero.
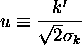 so that
so that 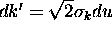 , we have
, we have
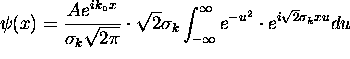 =
= 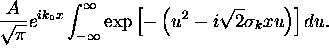 Completing the square,
Completing the square, 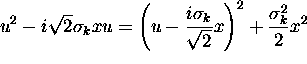 , giving
, giving
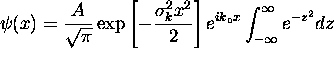 where
where 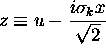 The definite integral has the value
The definite integral has the value
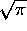 (look it up in a table of integrals!) giving
(look it up in a table of integrals!) giving
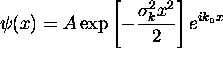 or
or 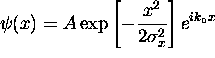 where
where 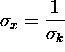 That is, the rms width of the wave packet about its
initial mean of
That is, the rms width of the wave packet about its
initial mean of 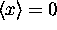 is
is
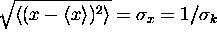 and the product of the x and k widths obeys the
uncertainty relation
and the product of the x and k widths obeys the
uncertainty relation
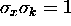 at t = 0.
at t = 0.
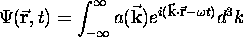 where we must remember that
where we must remember that
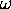 is a function of
is a function of
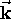 ,
not just a constant; the dispersion relation
,
not just a constant; the dispersion relation
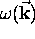 determines all the key physical properties of the wave such as
phase velocity
determines all the key physical properties of the wave such as
phase velocity
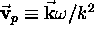 and
group (physical) velocity
and
group (physical) velocity
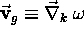 .
.
 direction, giving
the 1-dimensional version
direction, giving
the 1-dimensional version
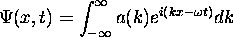 with
with 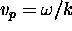 and
and
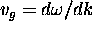 .
.
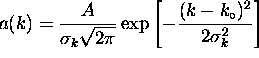 has a mean wavenumber
has a mean wavenumber 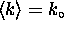 and a variance
and a variance 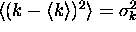 (so that
(so that 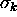 is the standard deviation of k).
is the standard deviation of k).
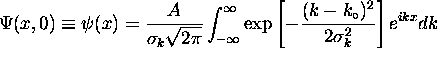 or
or 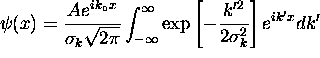 where
where 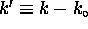
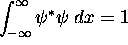 =
= 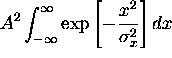 =
= 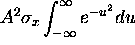 where
where 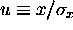 .
Again the definite integral equals
.
Again the definite integral equals
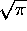 , giving
, giving
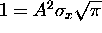 or
or
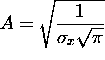 =
= 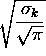 .
We have now fully described
.
We have now fully described 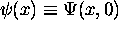 .
.
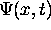 has a different k
and therefore progapates at a different velocity
has a different k
and therefore progapates at a different velocity
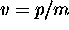 =
=
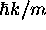 =
=
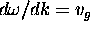 .
Thus they all move away from x = 0 at a different rate
and become spread out or dispersed
[hence the name "dispersion relation"
for
.
Thus they all move away from x = 0 at a different rate
and become spread out or dispersed
[hence the name "dispersion relation"
for 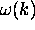 ]
relative to their average position
[the centre of the wave packet]
at
]
relative to their average position
[the centre of the wave packet]
at 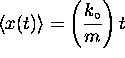 .
.
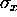 , therefore increases
with time from its minimum value
, therefore increases
with time from its minimum value
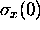 at t = 0.
The time dependence can be calculated with some effort
(not shown here);
the result is
at t = 0.
The time dependence can be calculated with some effort
(not shown here);
the result is
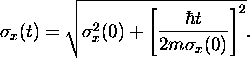
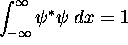 .
Thus the probability of finding the particle within dx of
its mean position
.
Thus the probability of finding the particle within dx of
its mean position 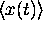 steadily decreases with time as the wave packet disperses.
steadily decreases with time as the wave packet disperses.
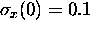 nm
(roughly atomic dimensions)
in a gaussian wave packet. For simplicity we will let
nm
(roughly atomic dimensions)
in a gaussian wave packet. For simplicity we will let
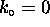 ;
that is, the electron is (on average) at rest.
If the electron is free
(as we have assumed throughout this treatment)
then its wave packet will expand to
;
that is, the electron is (on average) at rest.
If the electron is free
(as we have assumed throughout this treatment)
then its wave packet will expand to
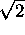 times its initial size
in a time
times its initial size
in a time 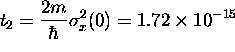 s.
s.
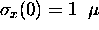 m,
the time required for it to disperse until
m,
the time required for it to disperse until
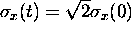 is
is
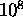 times longer:
times longer:
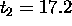 ns.
ns.
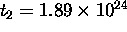 s.
(That is,
s.
(That is, 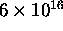 years!)
years!)