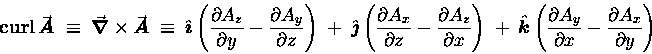

Next: The LAPLACIAN Operator
Up: Vector Calculus
Previous: DIVERGENCE of a Vector Field
If we form the vector ("cross") product
of  with a vector function
with a vector function
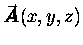 we get a vector result called the curl of
we get a vector result called the curl of 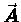 :
:
This is a lot harder to visualize than the DIVERGENCE,
but not impossible. Suppose you are in a boat in a huge river
(or Pass) where the current flows mainly in the x direction
but where the speed of the current (flux of water) varies with y.
Then if we call the current 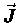 ,
we have a nonzero value
for the derivative
,
we have a nonzero value
for the derivative
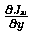 ,
which
you will recognize as one of the terms in the formula for
,
which
you will recognize as one of the terms in the formula for 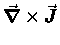 .
What does this imply? Well, if you are sitting in the boat,
moving with the current, it means the current on your port side
moves faster - i.e. forward relative to the boat -
and the current on your starboard side moves slower -
i.e. backward relative to the boat - and this implies a
circulation of the water around the boat -
i.e. a whirlpool! So
.
What does this imply? Well, if you are sitting in the boat,
moving with the current, it means the current on your port side
moves faster - i.e. forward relative to the boat -
and the current on your starboard side moves slower -
i.e. backward relative to the boat - and this implies a
circulation of the water around the boat -
i.e. a whirlpool! So 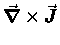 is a measure of
the local "swirliness" of the current
is a measure of
the local "swirliness" of the current 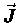 ,
which
means "curl" is not a bad name after all!
,
which
means "curl" is not a bad name after all!


Next: The LAPLACIAN Operator
Up: Vector Calculus
Previous: DIVERGENCE of a Vector Field
Jess H. Brewer -
Last modified: Wed Nov 18 12:24:39 PST 2015
![]() with a vector function
with a vector function
![]() we get a vector result called the curl of
we get a vector result called the curl of ![]() :
: