

Next: Rotational Analogies
Up: Rigid Bodies
Previous: Rigid Bodies
Just as in the translational [straight-line motion]
part of Mechanics there is an inertial factor m
which determines how much p you get
for a given
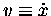 and how much
and how much
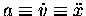 you get for a given F,
so in rotational Mechanics there is
an angular analogue of the inertial factor
that determines how much LO you get
for a given
you get for a given F,
so in rotational Mechanics there is
an angular analogue of the inertial factor
that determines how much LO you get
for a given
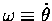 and how much
and how much
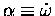 you get
for a given
you get
for a given 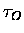 .
This angular inertial factor is called the
moment of inertia about O
[we must always specify the origin about which we are
defining torques and angular momentum] and is written
IO with the prescription
.
This angular inertial factor is called the
moment of inertia about O
[we must always specify the origin about which we are
defining torques and angular momentum] and is written
IO with the prescription
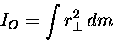 |
(11.21) |
where the integral represents a summation
over all little "bits" of mass dm
[we call these "mass elements"]
which are distances 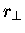 away from
an axis through the point O.
Here we discover a slight complication:
away from
an axis through the point O.
Here we discover a slight complication:
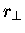 is measured from the axis,
not from O itself. Thus a mass element dm
that is a long way from O but right on the axis
will contribute nothing to IO.
This continues to get more complicated until we have
a complete description of Rotational Mechanics
with IO as a tensor of inertia
and lots of other stuff I will never use again in this course.
I believe I will stop here and leave the finer points
of Rotational Mechanics for later Physics courses!
is measured from the axis,
not from O itself. Thus a mass element dm
that is a long way from O but right on the axis
will contribute nothing to IO.
This continues to get more complicated until we have
a complete description of Rotational Mechanics
with IO as a tensor of inertia
and lots of other stuff I will never use again in this course.
I believe I will stop here and leave the finer points
of Rotational Mechanics for later Physics courses!


Next: Rotational Analogies
Up: Rigid Bodies
Previous: Rigid Bodies
Jess H. Brewer -
Last modified: Sat Nov 14 12:47:07 PST 2015