![]() " . . . approaches . . . "
" . . . approaches . . . "
OPERATORS: (these all operate to the right)
![]() = partial derivative operator
= partial derivative operator
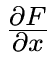 .
.
![]()
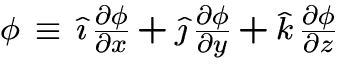
![]() = integral operator
= integral operator

LOGICAL SYMBOLS: (handy shorthand)
![]() " . . . is equivalent to . . . "
" . . . is equivalent to . . . "
... "Therefore . . . "
/ [a slash through any logical symbol]
denotes negation
(e.g.
![]() " . . . does not imply . . . ")
" . . . does not imply . . . ")