- . . . holds.1
-
In mathematics, a double negative really is positive.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . Laws:2
-
Note that division is not commutative:
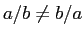 ! Neither is subtraction,
for that matter:
! Neither is subtraction,
for that matter:
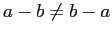 .
The Commutative Law for multiplication,
.
The Commutative Law for multiplication, 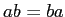 , holds for ordinary
numbers (real and imaginary) but it does not necessarily
hold for all the mathematical "things" for which some form of
"multiplication" is defined! For instance, the group
of rotation operators in 3-dimensional space is not
commutative - think about making two successive rotations of a
rigid object about perpendicular axes in different order and
you will see that the final result is different! This seemingly
obscure property turns out to have fundamental significance.
, holds for ordinary
numbers (real and imaginary) but it does not necessarily
hold for all the mathematical "things" for which some form of
"multiplication" is defined! For instance, the group
of rotation operators in 3-dimensional space is not
commutative - think about making two successive rotations of a
rigid object about perpendicular axes in different order and
you will see that the final result is different! This seemingly
obscure property turns out to have fundamental significance.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . consistent3
- In
Mathematics we never worry about such things;
all our symbols represent pure numbers;
but in Physics we usually have to express
the value of some physical quantity in units which
make sense and are consistent with the units of other
physical quantities symbolized in the same equation!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . generally4
- The
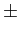 symbol means that both signs (+ and
symbol means that both signs (+ and 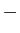 )
should represent legitimate answers.
)
should represent legitimate answers.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.