BELIEVE   ME   NOT!    - -     A   SKEPTIC's   GUIDE  

The Wave Equation

This is a bogus "derivation" in that we start with a solution to the WAVE EQUATION and then show what sort of differential equation it satisfies. Of course, once we have the equation we can work in the other direction, so this is not so bad . . . .

Suppose we know that we have a traveling wave  $A(x, t) \; = \; A_{_0} \; \cos(k x - \omega t)$.

At a fixed position  ($x=$ const)  we see SHM in time:

$$\left( \partial^2 A \over \partial t^2 \right)_x \, = \; - \, \omega^2 \, A$$ (14.8)

(Read: "The second partial derivative of $A$ with respect to time [i.e. the acceleration of $A$] with $x$ held fixed is equal to $-\omega^2$ times $A$ itself.") I.e. we must have a linear restoring force.

Similarly, if we take a "snapshot" (hold $t$ fixed) and look at the spatial variation of $A$, we find the oscillatory behaviour analogous to SHM,

$$\left( \partial^2 A \over \partial x^2 \right)_t \, = \; - \, k^2 \, A$$ (14.9)

(Read: "The second partial derivative of $A$ with respect to position [i.e. the curvature of $A$] with $t$ held fixed is equal to $-k^2$ times $A$ itself.")

Thus

$$A \, = \; -{1 \over \omega^2} \left( \partial^2 A \over \ . . . . . . ver k^2} \left( \partial^2 A \over \partial x^2 \right)_t .$$

If we multiply both sides by $-k^2$, we get

$${k^2 \over \omega^2} \left( \partial^2 A \over \partial t . . . . . . x \, = \; \left( \partial^2 A \over \partial x^2 \right)_t .$$

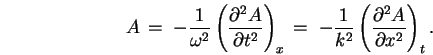
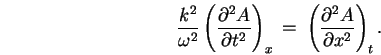
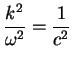But  $\omega = c k$  so   ${\displaystyle {k^2 \over \omega^2} = {1 \over c^2} }$,  giving the WAVE EQUATION:

$$\mbox{ \fbox{ \rule[-1.25\baselineskip]{0pt}{3\baselineskip . . . . . . c^2} \; {\partial^2 A \over \partial t^2} \; = \; 0 }$~ }}$$ (14.10)

In words, the curvature of $A$ is equal to $1/c^2$ times the acceleration of $A$ at any $(x,t)$ point (what we call an event in spacetime).

Whenever you see this differential equation governing some quantity $A$, i.e. where the acceleration of $A$ is proportional to its curvature, you know that $A(x,t)$ will exhibit wave motion!