THE UNIVERSITY OF
BRITISH COLUMBIA
PHYSICS 455
Lecture # 5 :
Wed. 15 Jan. 1997
The Boltzmann Distribution
LOGISTICS:
Assignment 1 is nominally due today,
but almost no one has turned it in yet.
Since there are no solutions (or ``right answers'') to this first
assignment, I can accept them any time right up to the last day
of classes (there must be some limit!) - but of course
it is not in your interest to let assigments pile up....
What do people think about having a take-home final exam?
Several options are possible;
if you can reach a consensus on the P455 WebCT Bulletin Board
(which see!)
in time for me to make plans, I will try to implement your choice.
HANDOUTS: Assignment 2 - due next Wed.
READING: You should be finished with Ch. 1 and Ch. 2
and starting on Ch. 3 now.
I. Recapitulate:
Actually some of the material described here as being part of Lecture 4
was really delivered in Lecture 5. Once I start writing up the lecture
descriptions there is no bell to stop me from going on ``after the hour.''
II. ADIABATIC DEMAGNETIZATION:
- For a large system of N independent spin-½ particles,
each of magnetic moment m, in a magnetic field B,
the equilibrium fractional magnetization
was shown to have the value
M/mN = mB/
 in the limit of high temperature (it can never actually get
larger than 100% spin polarization, of course).
This corresponds to a net spin energy of
U = Nm2B2/
in the limit of high temperature (it can never actually get
larger than 100% spin polarization, of course).
This corresponds to a net spin energy of
U = Nm2B2/ so
U2 = N2m4B4
/
so
U2 = N2m4B4
/ 2.
If we plug this back into
2.
If we plug this back into
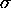 =
=
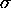 o -
U2/2m2B2N
and pretend that the thermal equilibrium value of U
is actually the value of U, we get
o -
U2/2m2B2N
and pretend that the thermal equilibrium value of U
is actually the value of U, we get
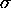 =
=
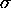 o -
N m2 B2
/ 2
o -
N m2 B2
/ 2  2 .
2 .
- Now suppose we prepare such a system in a field B
and let it come to thermal equilibrium with a large heat reservoir
(usually known as ``the lattice'' in recognition that most spin
systems are incorporated into crystalline solids). This may take
a while for the systems we are interested in, since the next step
is to reduce the magnetic field so rapidly that
the spins cannot ``relax'' to their new thermal equilibrium
polarization during the change. That is, the microscopic state
of the spin system does not change during this process, nor,
therefore, does the entropy. Such a process is called
isentropic or (equivalently) adiabatic.
- In the formula above, the entropy is a function only of
the ratio of B to
 .
Therefore if
.
Therefore if 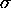 stays constant
while B is reduced by some factor, then
stays constant
while B is reduced by some factor, then
 gets reduced by the same factor.
In such a process the temperature of the spin system
is abruptly decreased by the same factor as the magnetic field.
gets reduced by the same factor.
In such a process the temperature of the spin system
is abruptly decreased by the same factor as the magnetic field.
- If one then waits for the spin system to come into thermal
equilibrium with the lattice, the lattice temperature will drop
as the spin system warms up. This method is used to cool from
a few milliKelvin (mK) - the practical lower limit of most
3He/4He dilution regrigerators
(about which we will learn more later) -
to a fraction of a mK, using paramagnetic salts.
- Because our high temperature approximation breaks down
when mB approaches
 (the spins cannot be more than 100% polarized)
the limit on the starting temperature
(the spins cannot be more than 100% polarized)
the limit on the starting temperature
 initial
depends upon the magnetic moment m and the field B.
For paramagnetic moments m
initial
depends upon the magnetic moment m and the field B.
For paramagnetic moments m 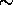 µB =
9.274
µB =
9.274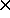 10-21
erg/G, while kB =
1.381
10-21
erg/G, while kB =
1.381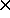 10-16
erg/K, so Tinitial[K]
10-16
erg/K, so Tinitial[K] 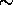 Binitial[G]/104. That is, for a
10,000 G [1 T] initial field one can cool from no lower than
about 1 K.
Binitial[G]/104. That is, for a
10,000 G [1 T] initial field one can cool from no lower than
about 1 K.
To start from even lower  initial
one can use adiabatic nuclear demagnetization, for which typical
magnetic moments are several thousand times weaker. Then one may
start from 1 mK at 3 T and cool into the microKelvin (µK) range.
The coldest temperatures ever achieved in laboratories on Earth
use huge refrigerators several stories high (with elaborate vibration-free
mountings) with a final stage based on adiabatic nuclear demagnetization.
initial
one can use adiabatic nuclear demagnetization, for which typical
magnetic moments are several thousand times weaker. Then one may
start from 1 mK at 3 T and cool into the microKelvin (µK) range.
The coldest temperatures ever achieved in laboratories on Earth
use huge refrigerators several stories high (with elaborate vibration-free
mountings) with a final stage based on adiabatic nuclear demagnetization.
-
III. Boltzmann Distribution and Partition Function:
- (See text.) A large thermal reservoir is placed in thermal contact
with a small system in a fully specified microscopic quantum state
|
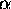 > of energy
> of energy

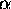 .
The total energy of the two combined systems is U and so the energy
of the reservoir is UR =
U -
.
The total energy of the two combined systems is U and so the energy
of the reservoir is UR =
U - 
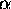 .
The probability P
.
The probability P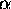 of such a configuration is proportional to the
product of the multiplicities for the two systems:
gR for the reservoir and 1 for the
fully specified state. Thus
P
of such a configuration is proportional to the
product of the multiplicities for the two systems:
gR for the reservoir and 1 for the
fully specified state. Thus
P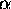
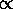 gR(U-
gR(U-
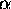 )
= exp(
)
= exp(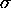 R(U) -
[
R(U) -
[
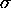 R
/
R
/ UR]
UR]

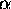 )
)
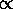 exp(-
exp(-
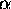 /
/ ) .
(Recall the definition of
) .
(Recall the definition of  )
This is called the Boltzmann factor.
)
This is called the Boltzmann factor.
- We would like to normalize the Boltzmann factor
to turn it into the actual probability
P
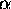 of finding
the small system in that particular microscopic quantum state.
To do so, we much divide by the sum of all such factors:
P
of finding
the small system in that particular microscopic quantum state.
To do so, we much divide by the sum of all such factors:
P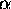 =
exp(-
=
exp(-
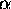 /
/ )/Z,
where
)/Z,
where
Z 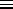

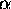 exp(-
exp(-
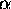 /
/ )
)
This is called the partition function for the small system.
- A little algebra converts the formula for the
thermal average energy of the small system from its obvious definition
< U > 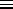

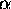

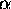 exp(-
exp(-
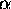 /
/ )
)
into the somewhat more compact form
< U > =  2
2
 (log Z)/
(log Z)/
 .
.
Subsequently we shall tend to ignore the distinction between the actual
energy U of such a small system and its thermal average
energy < U >.
- The same logic used to derive the Boltzmann factor
can be used to explain the Overhauser effect
(see text, Problem 5 in Ch. 3) is which, by contriving to add
evergy to the reservoir every time it gives up an energy

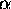 to the small system, a device can cause higher energy states of a system
to be more likely than lower energy states even though the system
is nominally in thermal equilibrium with a large reservoir.
to the small system, a device can cause higher energy states of a system
to be more likely than lower energy states even though the system
is nominally in thermal equilibrium with a large reservoir.
- In another problem (K&K Ch. 3, Problem 4)
we see how to use the obvious definition of the rms deviation of the energy
from its mean value to derive a formula for the variance
of the energy at a given temperature:
var U 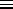 < (U - < U > )2 > =
< (U - < U > )2 > =
 2
2
 U/
U/
 .
.
Last modified: Sun Feb 2 13:35:56 PST
 in the limit of high temperature (it can never actually get
larger than 100% spin polarization, of course).
This corresponds to a net spin energy of
U = Nm2B2/
in the limit of high temperature (it can never actually get
larger than 100% spin polarization, of course).
This corresponds to a net spin energy of
U = Nm2B2/ so
U2 = N2m4B4
/
so
U2 = N2m4B4
/ 2.
If we plug this back into
2.
If we plug this back into
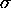 =
=
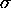 o -
U2/2m2B2N
and pretend that the thermal equilibrium value of U
is actually the value of U, we get
o -
U2/2m2B2N
and pretend that the thermal equilibrium value of U
is actually the value of U, we get
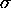 =
=
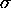 o -
N m2 B2
/ 2
o -
N m2 B2
/ 2  2 .
2 .
 .
Therefore if
.
Therefore if 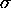 stays constant
while B is reduced by some factor, then
stays constant
while B is reduced by some factor, then
 gets reduced by the same factor.
In such a process the temperature of the spin system
is abruptly decreased by the same factor as the magnetic field.
gets reduced by the same factor.
In such a process the temperature of the spin system
is abruptly decreased by the same factor as the magnetic field.
 (the spins cannot be more than 100% polarized)
the limit on the starting temperature
(the spins cannot be more than 100% polarized)
the limit on the starting temperature
 initial
depends upon the magnetic moment m and the field B.
For paramagnetic moments m
initial
depends upon the magnetic moment m and the field B.
For paramagnetic moments m 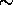 µB =
9.274
µB =
9.274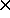 10-21
erg/G, while kB =
1.381
10-21
erg/G, while kB =
1.381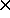 10-16
erg/K, so Tinitial[K]
10-16
erg/K, so Tinitial[K] 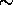 Binitial[G]/104. That is, for a
10,000 G [1 T] initial field one can cool from no lower than
about 1 K.
Binitial[G]/104. That is, for a
10,000 G [1 T] initial field one can cool from no lower than
about 1 K.
 initial
one can use adiabatic nuclear demagnetization, for which typical
magnetic moments are several thousand times weaker. Then one may
start from 1 mK at 3 T and cool into the microKelvin (µK) range.
The coldest temperatures ever achieved in laboratories on Earth
use huge refrigerators several stories high (with elaborate vibration-free
mountings) with a final stage based on adiabatic nuclear demagnetization.
initial
one can use adiabatic nuclear demagnetization, for which typical
magnetic moments are several thousand times weaker. Then one may
start from 1 mK at 3 T and cool into the microKelvin (µK) range.
The coldest temperatures ever achieved in laboratories on Earth
use huge refrigerators several stories high (with elaborate vibration-free
mountings) with a final stage based on adiabatic nuclear demagnetization.
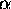 > of energy
> of energy

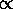 gR(U-
gR(U-