This is a relatively [pun intended] short Assignment, since
the first Midterm Exam is on Monday February 6
(in class, 50 minutes). Nevertheless it will count
the same as other Assignments, if you choose to tackle it.
For the exam, you may bring your own 1-page summary sheet
with any hard-to-remember equations etc.
The exam will cover all of Chapters 7 and 8,
sections 10.1 of Chapter 10, and all of Chapter 12.
There will not be anything on the Midterm explicitly about 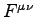 (second problem below) but applications of Eqs. (12.108)
are fair game.
(second problem below) but applications of Eqs. (12.108)
are fair game.
- If we stay in the Lorentz gauge (
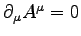 ),
),
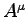 is a genuine 4-vector and therefore
is a genuine 4-vector and therefore 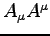 is
a Lorentz scalar. Use this fact to show that, in any frame,
is
a Lorentz scalar. Use this fact to show that, in any frame,
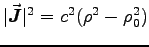 , where
, where 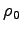 is the
charge density in the frame where
is the
charge density in the frame where 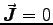 .
.
- Use the formal definition of the FIELD TENSOR
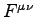 in Eq. (12.118)1 and the rule for its Lorentz transformation,2
in Eq. (12.118)1 and the rule for its Lorentz transformation,2
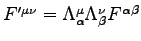 ,
to derive the equations analogous to Eqs. (12.108)
describing the transformation of
,
to derive the equations analogous to Eqs. (12.108)
describing the transformation of 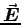 and
and 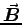 under a "boost" into a reference frame moving at velocity u
(with the usual corresponding definitions of
under a "boost" into a reference frame moving at velocity u
(with the usual corresponding definitions of 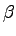 and
and 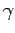 )
in the positive
)
in the positive 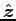 direction.3
direction.3
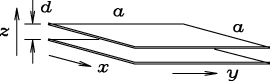
- A capacitor made from two square parallel plates a on a side
and d apart is given a charge -Q on the upper plate and +Q
on the lower plate. Let the origin of coordinates be in the centre
of the capacitor, the edges of the plates parallel to
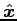 and
and
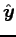 and the gap in the
and the gap in the 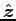 direction.
direction.
Using Lorentz transformations, find 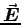 and
and 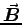 inside the capacitor
inside the capacitor
- in a frame moving at a velocity u in the
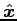 direction;
direction;
- in a frame moving at a velocity u in the
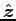 direction.
direction.
- For the former case, compare your result with what you would
expect from simply transforming the dimensions of the plates
into the moving frame and treating their motion as sheets of current.
Jess H. Brewer
2006-01-29

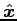 direction;
direction;
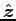 direction.
direction.