- . . . Eq. (12.118)1
- Let's acquiesce to
Griffiths' notation for this problem.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . transformation,2
- The Einstein
summation convention is assumed: sum over all repeated indices.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . direction.3
- Eqs. (12.108)
are for a "boost" in the
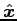 direction.
This is rather tedious, especially since the result is rather
obvious when you're done, but everyone should do it once
in order to understand that the definition of
direction.
This is rather tedious, especially since the result is rather
obvious when you're done, but everyone should do it once
in order to understand that the definition of 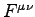 is more useful formally (for elegantly expressing the essence
of electromagnetism) than for solving practical problems.
is more useful formally (for elegantly expressing the essence
of electromagnetism) than for solving practical problems.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.