

Next: Power Dissipation
Up: AC Circuits
Previous: AC Circuits
We begin by picturing a generic series-LCR circuit driven by a
sinusoidal voltage
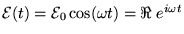 .
It is convenient to use the complex form21.2
for calculations;
just remember that none of the actual physical quantities
like current or voltage will actually have a measurable
imaginary part.21.3
The voltage amplitude
.
It is convenient to use the complex form21.2
for calculations;
just remember that none of the actual physical quantities
like current or voltage will actually have a measurable
imaginary part.21.3
The voltage amplitude
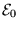 is taken to be pure real.
is taken to be pure real.
Figure:
An LCR circuit driven by an AC voltage.
![\begin{figure}~\\ [-0.5\baselineskip]
\begin{center}\mbox{\epsfig{file=PS/AC-LCR.ps,height=1.25in} }\end{center}\end{figure}](img6.gif) |
Applying Kirchhoff's rule of single-valued potential
around this loop, we have
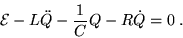 |
(21.1) |
When the AC power supply is first turned on,
we generally have a very complicated behaviour
involving the resonant (or "natural") frequency
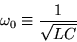 |
(21.2) |
and the damping rate
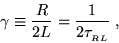 |
(21.3) |
just like the damped mass on a spring when an
oscillatory driving mechanism is applied.
If there were no resistor in the circuit,
this "ringing" would go on indefinitely;
but with the damping caused by R
it eventually dies away and the circuit settles down
to the only plausible "steady-state" motion,
namely for Q to oscillate at the same frequency
as the driving voltage:
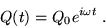 |
(21.4) |
Bearing in mind that the constant amplitude Q0
may not be entirely real, let's see if this trial solution
(4)
"works" - i.e. satisfies the differential equation.
One motive for using the complex exponential form is that
it is so easy to take derivatives: each time derivative
of Q(t) just "pulls down" another factor of 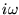 .
Thus
.
Thus
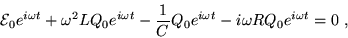 |
(21.5) |
from which we can remove the common factor
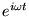 and do a little algebra to obtain
and do a little algebra to obtain
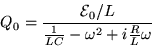 |
(21.6) |
or [recalling the definitions (2) and (3)]
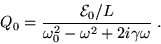 |
(21.7) |
Now, the charge on a capacitor cannot be measured directly;
what we usually want to know is the current
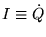 .
Since the entire time dependence of Q
is in the factor
.
Since the entire time dependence of Q
is in the factor
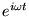 ,
we have trivially
,
we have trivially
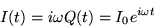 |
(21.8) |
where
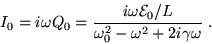 |
(21.9) |
Since everything we might want to know (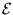 ,
Q and I)
has the same time dependence except for differences of phase
encoded in the complex amplitudes Q0 and I0, we can think
in terms of an effective resistance
,
Q and I)
has the same time dependence except for differences of phase
encoded in the complex amplitudes Q0 and I0, we can think
in terms of an effective resistance
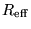 such that
such that
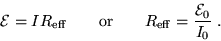 |
(21.10) |
With a little more algebra
we can write the effective resistance in the form
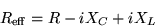 |
(21.11) |
where
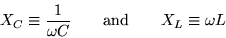 |
(21.12) |
are respectively the capacitive reactance
and the inductive reactance of the circuit.
These are quantities that "act like"
(and have the units of) resistances -
just like R, the first term in
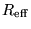 .
.
The current through the circuit
cannot be different in different places (due to charge conservation)
and is always in phase with the driving voltage.
This is not necessarily the case for the
voltage drops across R, C and L:
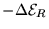 |
= |
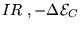 |
(21.13) |
From Eqs. (11) and (13)
one can easily deduce the phase differences
between these voltages at any time
(for example,
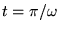 )
when
)
when 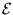 has its maximum negative real value:
the voltage drop across R will be real and positive
(it is always exactly out of phase with the driving voltage)
but the voltage drop across the inductance will be
in the positive imaginary direction -
i.e. its real part will be zero at that instant,
as will that of the voltage drop across the capacitor,
which is then in the negative imaginary direction.
has its maximum negative real value:
the voltage drop across R will be real and positive
(it is always exactly out of phase with the driving voltage)
but the voltage drop across the inductance will be
in the positive imaginary direction -
i.e. its real part will be zero at that instant,
as will that of the voltage drop across the capacitor,
which is then in the negative imaginary direction.
Figure:
The "Phase Circle".
![\begin{figure}~\\ [-0.5\baselineskip]
\begin{center}\mbox{\epsfig{file=PS/phase_circle.ps,height=2.25in} }\end{center}\end{figure}](img27.gif) |
A convenient way of looking at this is with the "Phase Circle"
shown in Fig. 21.2, where
the "directions" of the voltage drops
in "complex phase space" are shown as vectors.
All three voltage drops "rotate" in this "phase space"
at a constant frequency 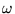 but their phase relationship
is always preserved: namely, the voltage across the
capacitor lags that across the resistor
by an angle of
but their phase relationship
is always preserved: namely, the voltage across the
capacitor lags that across the resistor
by an angle of 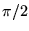 and the voltage across the
inductance leads that across the resistor
by an angle of
and the voltage across the
inductance leads that across the resistor
by an angle of 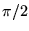 .21.4
At any other instant the real, measurable value of any of these
voltages is just its real part, i.e. the projection of its
complex vector onto the real axis.
.21.4
At any other instant the real, measurable value of any of these
voltages is just its real part, i.e. the projection of its
complex vector onto the real axis.


Next: Power Dissipation
Up: AC Circuits
Previous: AC Circuits
Jess H. Brewer -
Last modified: Mon Nov 16 18:20:42 PST 2015
![]() .
It is convenient to use the complex form21.2
for calculations;
just remember that none of the actual physical quantities
like current or voltage will actually have a measurable
imaginary part.21.3
The voltage amplitude
.
It is convenient to use the complex form21.2
for calculations;
just remember that none of the actual physical quantities
like current or voltage will actually have a measurable
imaginary part.21.3
The voltage amplitude
![]() is taken to be pure real.
is taken to be pure real.
![]() .
Since the entire time dependence of Q
is in the factor
.
Since the entire time dependence of Q
is in the factor
![]() ,
we have trivially
,
we have trivially
![]() ,
Q and I)
has the same time dependence except for differences of phase
encoded in the complex amplitudes Q0 and I0, we can think
in terms of an effective resistance
,
Q and I)
has the same time dependence except for differences of phase
encoded in the complex amplitudes Q0 and I0, we can think
in terms of an effective resistance
![]() such that
such that
![]() )
when
)
when ![]() has its maximum negative real value:
the voltage drop across R will be real and positive
(it is always exactly out of phase with the driving voltage)
but the voltage drop across the inductance will be
in the positive imaginary direction -
i.e. its real part will be zero at that instant,
as will that of the voltage drop across the capacitor,
which is then in the negative imaginary direction.
has its maximum negative real value:
the voltage drop across R will be real and positive
(it is always exactly out of phase with the driving voltage)
but the voltage drop across the inductance will be
in the positive imaginary direction -
i.e. its real part will be zero at that instant,
as will that of the voltage drop across the capacitor,
which is then in the negative imaginary direction.