BELIEVE   ME   NOT!    -     A   SKEPTIC's   GUIDE  

Rate of Change of a Vector

The derivative of a vector quantity   $\vec{\mbox{\boldmath$\space A $\unboldmath }}$  with respect to some independent variable  x  (of which it is a function) is defined in exactly the same way as the derivative of a scalar function:

$${d\vec{\mbox{\boldmath$ A $\unboldmath }} \over dx} \equiv . . . . . . - \vec{\mbox{\boldmath$ A $\unboldmath }}(x) \over \Delta x}$$ (10.1)

There is, however, a dramatic difference between scalar derivatives and vector derivatives: the latter can be nonzero even if the magnitude A of the vector $\vec{\mbox{\boldmath$\space A $\unboldmath }}$ remains constant. This is a consequence of the fact that vectors have two properties: magnitude and direction. If the direction changes, the derivative is nonzero, even if the magnitude stays the same!

This is easily seen using a sketch in two dimensions:

  

Figure: Note that the notation $\vec{\mbox{\boldmath$\space A $\unboldmath}}'$ does not denote the derivative of $\vec{\mbox{\boldmath$\space A $\unboldmath }}$ as it might in a Mathematics text.

In the case on the left, the vector $\vec{\mbox{\boldmath$\space A $\unboldmath}}'$ is in the same direction as $\vec{\mbox{\boldmath$\space A $\unboldmath }}$ but has a different length. [The two vectors are drawn side by side for visual clarity; try to imagine that they are on top of one another.] The difference vector $\Delta \vec{\mbox{\boldmath$\space A $\unboldmath }} \equiv \vec{\mbox{\boldmath$\space A $\unboldmath }}' - \vec{\mbox{\boldmath$\space A $\unboldmath }}$ is parallel to both $\vec{\mbox{\boldmath$\space A $\unboldmath }}$ and $\vec{\mbox{\boldmath$\space A $\unboldmath}}'$.^10.2 If we divide $\Delta \vec{\mbox{\boldmath$\space A $\unboldmath }}$ by the change $\Delta x$ in the independent variable (of which $\vec{\mbox{\boldmath$\space A $\unboldmath }}$ is a function) and let $\Delta x \to 0$ then we find that the derivative ${\displaystyle {d\vec{\mbox{\boldmath$\space A $\unboldmath }} \over dx} }$ is also $\parallel \vec{\mbox{\boldmath$\space A $\unboldmath }}$.

In the case on the right, the vector $\vec{\mbox{\boldmath$\space A $\unboldmath}}'$ has the same length (A) as $\vec{\mbox{\boldmath$\space A $\unboldmath }}$ but is not in the same direction. The difference $\Delta \vec{\mbox{\boldmath$\space A $\unboldmath }} \equiv \vec{\mbox{\boldmath$\space A $\unboldmath }}' - \vec{\mbox{\boldmath$\space A $\unboldmath }}$ formed by the "tip-to-tip" rule of vector subtraction is also no longer in the same direction as $\vec{\mbox{\boldmath$\space A $\unboldmath }}$. In fact, it is useful to note that for these conditions (constant magnitude A), as the difference $\Delta \vec{\mbox{\boldmath$\space A $\unboldmath }}$ becomes infinitesimally small it also becomes perpendicular to both $\vec{\mbox{\boldmath$\space A $\unboldmath }}$ and $\vec{\mbox{\boldmath$\space A $\unboldmath}}'$.^10.3 Thus the rate of change ${\displaystyle {d\vec{\mbox{\boldmath$\space A $\unboldmath }} \over dx} }$ of a vector $\vec{\mbox{\boldmath$\space A $\unboldmath }}$ whose magnitude A is constant will always be perpendicular to the vector itself: ${\displaystyle {d\vec{\mbox{\boldmath$\space A $\unboldmath }} \over dx} \perp \vec{\mbox{\boldmath$ A $\unboldmath }} }$ 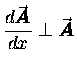if A is constant.