

Next: Rate of Change of a Vector
Up: Circular Motion
Previous: Circular Motion
Figure:
[top] Definition of the angle
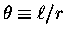 .
[bottom] Illustration of the trigonometric functions
.
[bottom] Illustration of the trigonometric functions
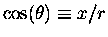 ,
,
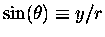 ,
tan(
,
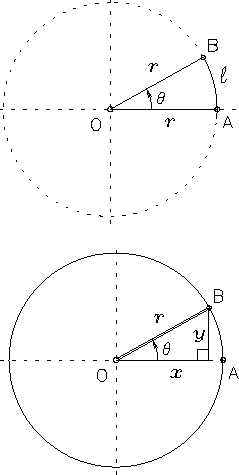
tan(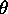 ) = y/x
etc.
describing the position of a point B in circular motion
about the centre at O.
) = y/x
etc.
describing the position of a point B in circular motion
about the centre at O.
 |
In Physics, angles are measured in radians.
There is no such thing as a "degree," although
Physicists will sometimes grudgingly admit that
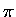 is equivalent to
is equivalent to 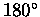 .
The angle
.
The angle 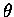 shown in Fig. 10.1
is defined as the dimensionless ratio
of the distance
shown in Fig. 10.1
is defined as the dimensionless ratio
of the distance 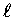 travelled along the circular arc
to the radius r of the circle.
There is a good reason for this.
The trigonometric functions
travelled along the circular arc
to the radius r of the circle.
There is a good reason for this.
The trigonometric functions
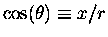 ,
,
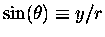 ,
tan(
,
tan(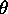 ) = y/x
etc.
are themselves defined as dimensionless ratios
and their argument (
) = y/x
etc.
are themselves defined as dimensionless ratios
and their argument (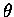 )
ought to be
a dimensionless ratio (a "pure number") too,
so that these functions can be expressed as
power series in
)
ought to be
a dimensionless ratio (a "pure number") too,
so that these functions can be expressed as
power series in 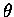 :
:
![$
\begin{array}[c]{rrrrrrrr}
\cos(\theta) =& 1 &
&- {\displaystyle {\theta^2 . . .
. . . \over 3!} }
& &+ {\displaystyle {\theta^5 \over 5!} }
& \cdots
\end{array}$](img10.gif)
Why would anyone want to do this? You'll see, heh, heh . . . .
Jess H. Brewer -
Last modified: Sat Nov 14 12:23:07 PST 2015


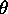 ) = y/x
etc.
are themselves defined as dimensionless ratios
and their argument (
) = y/x
etc.
are themselves defined as dimensionless ratios
and their argument (![$
\begin{array}[c]{rrrrrrrr}
\cos(\theta) =& 1 &
&- {\displaystyle {\theta^2 . . .
. . . \over 3!} }
& &+ {\displaystyle {\theta^5 \over 5!} }
& \cdots
\end{array}$](img10.gif)