BELIEVE   ME   NOT!    -     A   SKEPTIC's   GUIDE  

Relativistic Energy

Let's generalize our formula for kinetic energy so that it is relativistically correct. For a massless particle (like a photon) the expression (4) doesn't make any sense and is in fact wrong. Without stopping now to explain where it comes from, I will just give you the relativistically correct and completely general formula for the total energy of a particle:

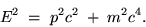$$E^2 \; = \; p^2 c^2 \; + \; m^2 c^4 .$$ (24.16)

Note that this TOTAL RELATIVISTIC ENERGY has the irreducible value E₀ = m c² when the particle is at rest (momentum = zero). This should ring a bell. To separate the KINETIC ENERGY K from the total relativistic energy we just subtract off E₀.

It turns out [Don't you love that phrase?] that de Broglie's relation (1) is relativistically correct! Thus we can still use it to calculate the total energy even if the confined particle is ultrarelativistic or massless. In fact, any particle acts pretty much like a photon at high enough momentum, where we can ignore m² c⁴ in comparison with p² c², in which case the formula simplifies to E = pc or (for our ultrarelativistic particle in a box)

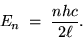$$E_n \; = \; {n h c \over 2 \ell} .$$ (24.17)