

Next: The Planck Length
Up: Relativistic Energy
Previous: Relativistic Energy
As long as we're being relativistic, why not go all the way?
Suppose a very lightweight particle is in orbit around a very
heavy mass m, attracted only by gravity. A simple application
of Newton's Second Law yields the ORBITAL VELOCITY
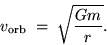 |
(24.18) |
Taking this at face value, what happens when
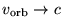 ?
For a given m, there is a radius called the
SCHWARZSCHILD RADIUS
?
For a given m, there is a radius called the
SCHWARZSCHILD RADIUS
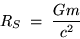 |
(24.19) |
for which anything close to the mass
cannot maintain its orbit without exceeding the speed of light.
Since this is impossible [I am being really sloppy and glib now,
but the conclusion is qualitatively correct] once anything gets
inside that radius it falls in the rest of the way and never
comes out. Even light. Hence the term, " BLACK HOLE".
Any mass m has its Rs; but usually the density
of a given lump of matter is not high enough to place sufficient
m inside a given r to cause a black hole to form.


Next: The Planck Length
Up: Relativistic Energy
Previous: Relativistic Energy
Jess H. Brewer -
Last modified: Wed Nov 18 17:31:11 PST 2015