

Next: Resonance
Up: Simple Harmonic Motion
Previous: Generalization of SHM
Why is SHM characteristic of such an enormous variety of phenomena?
Because for sufficiently small displacements from equilibrium,
every system with an equilibrium configuration satisfies
the first condition for SHM: the linear restoring force.
Here is the simple argument:
a linear restoring force is equivalent to a potential energy
of the form
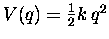 -- i.e. a
"quadratic minimum" of the potential energy at the
equilibrium configuration q = 0.
But if we "blow up" a graph of V(q) near q = 0,
every minimum looks quadratic under sufficient magnification!
That means any system that has
an equilibrium configuration also has some analogue of a
"potential energy" which is a minimum there;
if it also has some form of inertia so that
it tends to stay at rest (or in motion) until acted upon
by the analogue of a force, then it will automatically
exhibit SHM for small-amplitude displacements.
This makes SHM an extremely powerful paradigm.
-- i.e. a
"quadratic minimum" of the potential energy at the
equilibrium configuration q = 0.
But if we "blow up" a graph of V(q) near q = 0,
every minimum looks quadratic under sufficient magnification!
That means any system that has
an equilibrium configuration also has some analogue of a
"potential energy" which is a minimum there;
if it also has some form of inertia so that
it tends to stay at rest (or in motion) until acted upon
by the analogue of a force, then it will automatically
exhibit SHM for small-amplitude displacements.
This makes SHM an extremely powerful paradigm.
Jess H. Brewer -
Last modified: Sun Nov 15 13:51:11 PST 2015