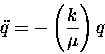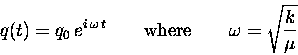

Next: The Universality of SHM
Up: Simple Harmonic Motion
Previous: Limiting Cases
As for all the other types of equations of motion,
SHM need not have anything to do with masses, springs
or even Physics. Even within Physics, however, there are
so many different kinds of examples of SHM that
we go out of our way to generalize the results:
using "q" to represent the "coordinate" whose
displacement from the equilibrium "position"
(always taken as q = 0) engenders some sort of
restoring "force"
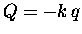 and "
and "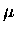 " to represent an "inertial factor"
that plays the rôle of the mass, we have
" to represent an "inertial factor"
that plays the rôle of the mass, we have
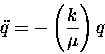 |
(13.26) |
for which the solution is the real part of
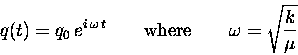 |
(13.27) |
When some form of "drag" acts on the system, we expect to see
the qualitative behaviour pictured in Fig. 13.5
and described by Eqs. (21) and (22).
Although one might expect virtually every real example
to have some sort of frictional damping term,
in fact there are numerous physical examples
with no damping whatsoever, mostly from the
microscopic world of solids.


Next: The Universality of SHM
Up: Simple Harmonic Motion
Previous: Limiting Cases
Jess H. Brewer -
Last modified: Sun Nov 15 13:50:31 PST 2015