

Next: Simple Harmonic Motion
Up: Sinusoidal Motion
Previous: Sinusoidal Motion
Figure:
Projected motion of a point on the rim of a wheel.
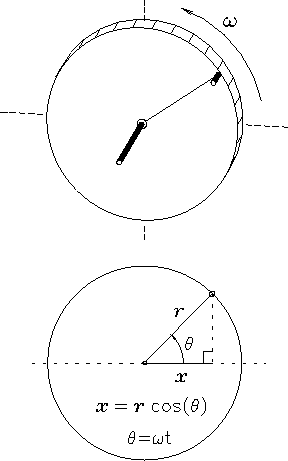 |
Imagine a rigid wheel rotating at constant angular velocity
about a fixed central axle. A bolt screwed into the rim of
the wheel executes uniform circular motion about the
centre of the axle.13.3
For reference we scribe a line on the wheel from the centre
straight out to the bolt and call this line the radius vector.
Imagine now that we take this apparatus outside at high noon
and watch the motion of the shadow of the bolt
on the ground. This is (naturally enough) called the
projection of the circular motion onto the
horizontal axis. At some instant the radius vector makes
an angle
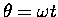 with the horizontal,
where
with the horizontal,
where 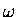 is the angular frequency of the wheel
(
is the angular frequency of the wheel
(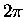 times the number of full revolutions per unit time)
and we measure the time t from the instant when the
radius vector is horizontal.
From a side view of the wheel we can see that the distance x
from the shadow of the central axle to the shadow of the bolt
[i.e. the projected horizontal displacement of the bolt
from the centre, where x=0] will be given by trigonometry
on the indicated right-angle triangle:
times the number of full revolutions per unit time)
and we measure the time t from the instant when the
radius vector is horizontal.
From a side view of the wheel we can see that the distance x
from the shadow of the central axle to the shadow of the bolt
[i.e. the projected horizontal displacement of the bolt
from the centre, where x=0] will be given by trigonometry
on the indicated right-angle triangle:
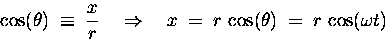 |
(13.1) |
The resultant amplitude of the displacement
as a function of time is shown in Fig. 13.3.
Figure:
The cosine function.
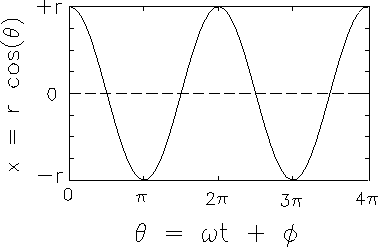 |
The horizontal velocity vx of the projected shadow
of the bolt on the ground can also be obtained by trigonometry
if we recall that the vector velocity 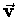 is always
perpendicular to the radius vector
is always
perpendicular to the radius vector 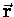 .
I will leave it as an exercise for the reader to show that
the result is
.
I will leave it as an exercise for the reader to show that
the result is
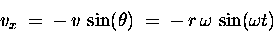 |
(13.2) |
where
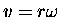 is the constant speed of the bolt
in its circular motion around the axle.
It also follows (by the same sorts of arguments) that
the horizontal acceleration ax of the bolt's shadow
is the projection onto the
is the constant speed of the bolt
in its circular motion around the axle.
It also follows (by the same sorts of arguments) that
the horizontal acceleration ax of the bolt's shadow
is the projection onto the 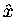 direction of
direction of
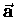 ,
which we know is back toward the centre of the wheel
-- i.e. in the
,
which we know is back toward the centre of the wheel
-- i.e. in the 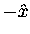 direction; its value at time t
is given by
direction; its value at time t
is given by
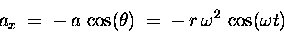 |
(13.3) |
where
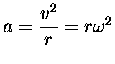 is the
magnitude of the centripetal acceleration of the bolt.
is the
magnitude of the centripetal acceleration of the bolt.


Next: Simple Harmonic Motion
Up: Sinusoidal Motion
Previous: Sinusoidal Motion
Jess H. Brewer -
Last modified: Sun Nov 15 13:34:45 PST 2015

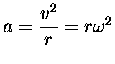 is the
magnitude of the centripetal acceleration of the bolt.
is the
magnitude of the centripetal acceleration of the bolt.