BELIEVE   ME   NOT!    -     A   SKEPTIC's   GUIDE  

The Binomial Distribution

To generalize, we talk about a system of  N  particles,^15.5 each of which can only be in one of two possible single-particle states. A fully specified  N-particle state of the system would have the single-particle state of each individual particle specified, and is not very interesting. The partially specified  N-particle state with  n  of the particles in the first single-particle state and the remaining  (N-n)  particles in the other single-particle state can be realized in   $\Omega(n,N)$  different ways, with   $\Omega(n,N)$  given by Eq. (1). Because there are only two possible single-particle states, this case of  $\Omega$  is called the binomial distribution. It is plotted^15.6 in Fig. 15.1 for several values of  N.

  

Figure: The normalized binomial distribution for several values of  N. In order to put several cases on a single graph, the horizontal axis shows  n  divided by its maximum possible value  N  [giving the fraction of the total range] and the binomial coefficient   $\Omega(n,N)$  given by Eq. (1) has been divided by the total number of possible fully specified N-particle states,  2^N,  to give the "normalized" probability - i.e. if we add up the values of   $\Omega(n,N)/2^N$  for all possible  n  from 0 to N, the total probability must be 1. [This is eminently sensible; the probability of  n  having some value is surely equal to unity!]

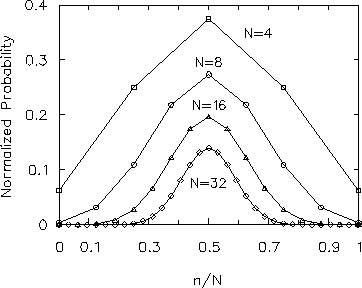Note what happens to   $\Omega(n,N)$  as  N  gets bigger: the peak value, which always occurs at   $n_{\rm peak} = \onehalf N$,  gets very large [in the plots it is compensated by dividing by  2^N,  which is a big number for large  N] and the width of the distribution grows steadily narrower - i.e. values of   ${n \over N}$  far away from the peak get less and less likely as  N  increases. The width is in fact the standard deviation^15.7 of a hypothetical random sample of  n,  and is proportional to  $\sqrt{N}$.  The fractional width (expressed as a fraction of the total range of  n,  namely  N) is therefore proportional to   ${\sqrt{N} \over N} \; = \; {1 \over \sqrt{N}}$:

$$\hbox{\rm Fractional Width} \; \propto \; {1 \over \sqrt{N}}$$ (15.2)

which means that for really large  N,  like   N = 10²⁰, the binomial distribution will get really narrow, like a part in 10¹⁰, in terms of the fraction of the average.