

Next: Linear Superposition
Up: Wavy Strings
Previous: Wavy Strings
One nice feature of waves in a taut string is that they explicitly
illustrate the phenomenon of polarization: if we change our
notation slightly to label the string's equilibrium direction
(and therefore the direction of propagation of a wave in the string)
as 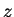 , then there are two orthogonal choices of "transverse"
direction:
, then there are two orthogonal choices of "transverse"
direction: 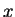 or
or 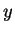 . We can set the string "wiggling" in
either transverse direction, which we call the two orthogonal
polarization directions.
. We can set the string "wiggling" in
either transverse direction, which we call the two orthogonal
polarization directions.
Of course, one can choose an infinite number of transverse
polarization directions, but these correspond to simple
superpositions of 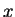 - and
- and 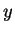 -polarized waves with
the same phase.
-polarized waves with
the same phase.
One can also superimpose 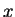 - and
- and 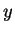 -polarized waves of the same
frequency and wavelength but with phases differing by
-polarized waves of the same
frequency and wavelength but with phases differing by 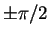 .
This gives left- and right-circularly polarized waves;
I will leave the mathematical description of such waves
(and the mulling over of its physical meaning)
as an "exercise for the student . . . . "
.
This gives left- and right-circularly polarized waves;
I will leave the mathematical description of such waves
(and the mulling over of its physical meaning)
as an "exercise for the student . . . . "
Jess H. Brewer -
Last modified: Sun Nov 15 18:01:29 PST 2015
![]() - and
- and ![]() -polarized waves with
the same phase.
-polarized waves with
the same phase.
![]() - and
- and ![]() -polarized waves of the same
frequency and wavelength but with phases differing by
-polarized waves of the same
frequency and wavelength but with phases differing by ![]() .
This gives left- and right-circularly polarized waves;
I will leave the mathematical description of such waves
(and the mulling over of its physical meaning)
as an "exercise for the student . . . . "
.
This gives left- and right-circularly polarized waves;
I will leave the mathematical description of such waves
(and the mulling over of its physical meaning)
as an "exercise for the student . . . . "