

Next: Standing Waves
Up: WAVES
Previous: Polarization
The above derivation relied heavily on the SMALL-ANGLE APPROXIMATIONS
which are valid only for small displacements of the string from
its equilibrium position (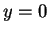 for all
for all 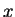 ).
This almost always true: the simple description of a wave given here
is only strictly valid in the limit of small displacements from equilibrium;
for large displacements we usually pick up "anharmonic" terms
corresponding to nonlinear restoring forces.
But as long as the restoring force stays linear we have an important
consequence: several different waves can propagate independently
through the same medium. (E.g. down the same string.)
The displacement at any given time and place is just the linear sum
of the displacements due to each of the simultaneously propagating waves.
This is known as the PRINCIPLE OF LINEAR SUPERPOSITION,
and it is essential to our understanding of wave phenomena.
).
This almost always true: the simple description of a wave given here
is only strictly valid in the limit of small displacements from equilibrium;
for large displacements we usually pick up "anharmonic" terms
corresponding to nonlinear restoring forces.
But as long as the restoring force stays linear we have an important
consequence: several different waves can propagate independently
through the same medium. (E.g. down the same string.)
The displacement at any given time and place is just the linear sum
of the displacements due to each of the simultaneously propagating waves.
This is known as the PRINCIPLE OF LINEAR SUPERPOSITION,
and it is essential to our understanding of wave phenomena.
In general the overall displacement 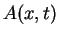 resulting from
the linear superposition of two waves
resulting from
the linear superposition of two waves
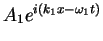 and
and
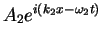 is given by
is given by
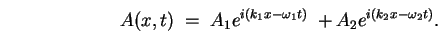 |
(14.17) |
Let's look at a few simple examples.
Subsections


Next: Standing Waves
Up: WAVES
Previous: Polarization
Jess H. Brewer -
Last modified: Sun Nov 15 18:02:11 PST 2015
![]() resulting from
the linear superposition of two waves
resulting from
the linear superposition of two waves
![]() and
and
![]() is given by
is given by