Effective target thickness

Because of the non-uniformity of the target observed in Section 3.3, the average layer thickness depends on the width and profile of the beam which stops in the target. Also recall that we have measured only the profile in the Y (vertical) dimension, hence the horizontal profile has to be assumed. The effective thickness can be defined via

(78)

where T_i is the thickness at the ith measured spot, and w_i the weighting factor. A weighted root-mean-square deviation of thickness is defined via

(79)

This is a quantitative measure of the non-uniformity and is useful when optimizing the vertical position of the diffuser for deposition.

Figure 6.1 illustrates the dependence of the effective thickness on the beam parameters. The average was calculated assuming rotational symmetry of the thickness profile, and weighted with two different beam parameterizations (i) Gaussian beam, and (ii) a flat top Gaussian, for which the radial intensity at the distance r, f(r) is defined by:

  

Figure 6.1: Dependence of the effective thickness (above) and the effective deviation (below) on the beam parameters and the radial cut-off values. (a) (b) (c): Flat-top Gaussian beam (FG, defined in Eq. 6.3) with and FWHM . (d) (e) (f): Gaussian beam (G) with FWHM_g = 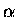$\alpha$. The points are slightly shifted horizontally for visual ease. The error bars represent the 5% uncertainty from the stopping power.

The figure also shows the dep