


Next: 3.2.4 Influence of the
Up: 3.2 Spin Relaxation in
Previous: 3.2.2 Low Temperature Behaviour
The temperature dependence of (3.9) discussed above
can be modified through several mechanisms which we will
consider in turn: anisotropy of  , finite lifetime
of quasi-particle excitations, and magnetic effects.
, finite lifetime
of quasi-particle excitations, and magnetic effects.
The consequences of anisotropy on the ratio
RS/RN are found by including an angular integral in
(3.9), and they can be most easily explained by a
comparison between the
angular average DOS, gA(E), and gS(E)
of (3.8).
where P(a) is the distribution of the anisotropy a of the gap
around the Fermi surface.
Even a small anisotropy, such
as that for aluminum[104], transforms the BCS singularity
in gS(E)
into a mild van Hove singularity at some average  ,and gA is still perfectly gapped with
gA(E)=0 for
,and gA is still perfectly gapped with
gA(E)=0 for  (see Fig. 3.12a).
The effect of anisotropy is thus to reduce the size of the
coherence peak in RS/RN and to modify the Arrhenius slope
relative to the isotropic case.
Extreme anisotropy, such as that for non-zero
angular momentum pairing states, is similar except that gA is
no longer gapped as there are nodes in
(see Fig. 3.12a).
The effect of anisotropy is thus to reduce the size of the
coherence peak in RS/RN and to modify the Arrhenius slope
relative to the isotropic case.
Extreme anisotropy, such as that for non-zero
angular momentum pairing states, is similar except that gA is
no longer gapped as there are nodes in  .For example, for a d-wave order parameter[108],
.For example, for a d-wave order parameter[108],
 as
as  .
Although gA is still peaked in this situation, the coherence peak
in RS/RN may be completely eliminated[109], and the
exponential temperature dependence is replaced by a power law
.
Although gA is still peaked in this situation, the coherence peak
in RS/RN may be completely eliminated[109], and the
exponential temperature dependence is replaced by a power law
 , where p = 2 for d-wave,
and other values of p are obtained[110] for different nodal
structures of
, where p = 2 for d-wave,
and other values of p are obtained[110] for different nodal
structures of  .This kind of behaviour has been observed[111,112] in
YBa2Cu3O6.95, for which there is strong evidence of a d-wave
.This kind of behaviour has been observed[111,112] in
YBa2Cu3O6.95, for which there is strong evidence of a d-wave
 .A p-wave
.A p-wave  may be the source of similar
temperature dependence in some Heavy Fermion
superconductors[113,114],
while one dimensionality may cause it in some organic
superconductors[115].
may be the source of similar
temperature dependence in some Heavy Fermion
superconductors[113,114],
while one dimensionality may cause it in some organic
superconductors[115].
Figure 3.12:
a) Models of the superconducting DOS:
BCS is gS of Eq.(3.8), Aniso is gA
(Eq.(3.11)) with a gate function
distribution P(a) of width 0.1 ,
,  is gD
(Eq.(3.12)) with
is gD
(Eq.(3.12)) with
 , and
, and  is gSC
(Eq.(3.13)) with
is gSC
(Eq.(3.13)) with
 .b) The value of the Hebel-Slichter integral for
the BCS and lifetime (Eq. (3.12)) broadened gS(E).
The magnetic inelasticity parameter (
.b) The value of the Hebel-Slichter integral for
the BCS and lifetime (Eq. (3.12)) broadened gS(E).
The magnetic inelasticity parameter ( ) is appropriate
for Mu@C60 in Rb3C60. The BCS temperature dependence
) is appropriate
for Mu@C60 in Rb3C60. The BCS temperature dependence  was used.
was used.
 |
Finite lifetime ( ) of the quasiparticle excitations of a superconductor
due, for example, to electron-phonon, electron-electron or impurity
scattering can also modify RS/RN.
This possibility was suggested by
Hebel and Slichter in their original work[95]
to explain the small size of the coherence peak they observed in Al.
They calculated a DOS which was a version of
Eq. (3.8) smeared by convolution with a gate function of
width
) of the quasiparticle excitations of a superconductor
due, for example, to electron-phonon, electron-electron or impurity
scattering can also modify RS/RN.
This possibility was suggested by
Hebel and Slichter in their original work[95]
to explain the small size of the coherence peak they observed in Al.
They calculated a DOS which was a version of
Eq. (3.8) smeared by convolution with a gate function of
width  .A detailed analysis of the temperature dependence of
RS/RN resulting from this approximation is given by Hebel[116].
A different Ansatz for the DOS was used by
Dynes et al.[117] to describe tunneling measurements:
.A detailed analysis of the temperature dependence of
RS/RN resulting from this approximation is given by Hebel[116].
A different Ansatz for the DOS was used by
Dynes et al.[117] to describe tunneling measurements:
where  . However, Allen and Rainer[118]
point out that for a lifetime due to electron-phonon scattering, one
must resort to the Eliashberg theory of strongly coupled superconductors
[52,119] in which the order parameter becomes complex,
and the DOS is[120]
. However, Allen and Rainer[118]
point out that for a lifetime due to electron-phonon scattering, one
must resort to the Eliashberg theory of strongly coupled superconductors
[52,119] in which the order parameter becomes complex,
and the DOS is[120]
where[121]  (
( is the imaginary part), and
is the imaginary part), and
 is determined by the Eliashberg theory and the
coupling constant-phonon spectrum product
is determined by the Eliashberg theory and the
coupling constant-phonon spectrum product  for the
particular material.
Fibich[122] first treated the problem of calculating
RS/RN using (3.13)
by neglecting the energy dependence of
for the
particular material.
Fibich[122] first treated the problem of calculating
RS/RN using (3.13)
by neglecting the energy dependence of  , and simply using
, and simply using
 evaluated at the energy which is most important for the
integral (3.9), i.e.
evaluated at the energy which is most important for the
integral (3.9), i.e.  .The temperature dependence for the imaginary
part
.The temperature dependence for the imaginary
part  due to phonon scattering[122,123] and
scattering from other quasiparticles[121,124] has been
calculated in the low temperature limit.
For the temperature dependence of the real part
due to phonon scattering[122,123] and
scattering from other quasiparticles[121,124] has been
calculated in the low temperature limit.
For the temperature dependence of the real part  (and for
the parameter
(and for
the parameter  in either of the preceding models) it is
reasonable[52] to assume that the temperature dependence
of the real part of the order parameter is
approximately that of the BCS
in either of the preceding models) it is
reasonable[52] to assume that the temperature dependence
of the real part of the order parameter is
approximately that of the BCS  .Recently, it has become feasible[125,118] to
calculate RS/RN using the full strong-coupling
.Recently, it has become feasible[125,118] to
calculate RS/RN using the full strong-coupling  ,thus avoiding these approximations. As input to such a calculation,
one would ideally first obtain a reasonable
form for
,thus avoiding these approximations. As input to such a calculation,
one would ideally first obtain a reasonable
form for  . However, according to Akis[125],
the details of
. However, according to Akis[125],
the details of  are not important, and
the most significant information in determining RS/RN(T) is summarized
in the ratio
are not important, and
the most significant information in determining RS/RN(T) is summarized
in the ratio  , where
, where  is the logarithmic moment
of
is the logarithmic moment
of  (Eq. (1.8)).
Note that the effect of impurities in the Eliashberg theory has recently been
revisited[126]. These authors find that ``vertex corrections'' from
impurity scattering can increase the size of the coherence peak as
the mean free path is reduced.
(Eq. (1.8)).
Note that the effect of impurities in the Eliashberg theory has recently been
revisited[126]. These authors find that ``vertex corrections'' from
impurity scattering can increase the size of the coherence peak as
the mean free path is reduced.
Magnetism may also influence
RS/RN(T), for instance,
in the classical example[127] of gaplessness in a superconductor
due to the presence of magnetic impurities,
the coherence peak can be reduced or eliminated and the
exponential fall-off strongly modified[128,129].
Superconductors that are intrinsically magnetic
exhibit similar strong deviations[113,130].
In regard to high-Tc superconductors,
antiferromagnetic correlations between quasiparticles
have also been shown[109,125] to damp the coherence peak.
However, it should be noted that
no anomalous behaviour connected with magnetism has been
reported yet in A3C60. Recently[131], the closely related
NH3K3C60 material which is superconducting under high pressure
has been found to exhibit a metal-insulator transition to a magnetic
state[132] at about 40K.
The small bandwidth and large coulomb
interactions between electrons also cause important correlation effects,
for example the magnetism in o-A1C60.
The proximity to a similar magnetic phase may be enhanced by the
analogous polymerization[133]
of the C60 anions in the Pa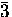 materials.
materials.



Next: 3.2.4 Influence of the
Up: 3.2 Spin Relaxation in
Previous: 3.2.2 Low Temperature Behaviour
![]() , finite lifetime
of quasi-particle excitations, and magnetic effects.
, finite lifetime
of quasi-particle excitations, and magnetic effects.

![]() ) of the quasiparticle excitations of a superconductor
due, for example, to electron-phonon, electron-electron or impurity
scattering can also modify RS/RN.
This possibility was suggested by
Hebel and Slichter in their original work[95]
to explain the small size of the coherence peak they observed in Al.
They calculated a DOS which was a version of
Eq. (3.8) smeared by convolution with a gate function of
width
) of the quasiparticle excitations of a superconductor
due, for example, to electron-phonon, electron-electron or impurity
scattering can also modify RS/RN.
This possibility was suggested by
Hebel and Slichter in their original work[95]
to explain the small size of the coherence peak they observed in Al.
They calculated a DOS which was a version of
Eq. (3.8) smeared by convolution with a gate function of
width ![]() .A detailed analysis of the temperature dependence of
RS/RN resulting from this approximation is given by Hebel[116].
A different Ansatz for the DOS was used by
Dynes et al.[117] to describe tunneling measurements:
.A detailed analysis of the temperature dependence of
RS/RN resulting from this approximation is given by Hebel[116].
A different Ansatz for the DOS was used by
Dynes et al.[117] to describe tunneling measurements:
![]() materials.
materials.