


Next: 2.3 Data Reduction
Up: 2.2 Hardware for Spectroscopy
Previous: 2.2 Hardware for Spectroscopy
By far the most common form of 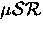 experiment operates in the
time differential mode.
An arrangement of detectors surrounding a sample
is shown schematically in Fig. 2.4.
experiment operates in the
time differential mode.
An arrangement of detectors surrounding a sample
is shown schematically in Fig. 2.4.
Figure 2.4:
Schematic diagram showing an arrangment of a
sample and five scintillation particle detectors.
Each muon triggers the thin muon (TM) detector on entering the experiment.
Later, the decay positron triggers one of the positron detectors.
 |
The positron detectors are usually mounted in pairs on opposite sides
of the sample; Back-Front, Left-Right and Up-Down, a geometry
well suited to extracting the signal, which we will come to shortly.
Clever variations on this scheme have been used for special
applications, to accomodate very small samples or very high
magnetic fields for example, but all of these perform
essentially the same function of detecting the angular distribution
of positrons.
We include in our example a magnetic field along the  -axis,
transverse to the
initial muon polarization so that the spins undergo Larmor
precession in the
-axis,
transverse to the
initial muon polarization so that the spins undergo Larmor
precession in the  plane until the muons decay.
Such experiments are termed transverse-field (TF) experiments,
giving a signal that demonstrates in an intuitive
way the analogy between
plane until the muons decay.
Such experiments are termed transverse-field (TF) experiments,
giving a signal that demonstrates in an intuitive
way the analogy between 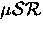 and traditional NMR.
One can also perform experiments with no (zero) external magnetic field (ZF)
or with a longitudinal field (LF) parallel to the initial muon spin,
with no other change to the experimental apparatus.
and traditional NMR.
One can also perform experiments with no (zero) external magnetic field (ZF)
or with a longitudinal field (LF) parallel to the initial muon spin,
with no other change to the experimental apparatus.
Each muon enters the experiment with a velocity of about 1/4 of the speed
of light, passing through a thin (0.125 mm) plastic
muon scintillation detector (TM) which provides a ``start" pulse
to the data acquisition electronics.
The muon then enters the sample a few cm further downstream,
where it comes to a stop and eventually decays.
When one of the positron detectors intercepts the outgoing positron,
a ``stop" pulse is generated and the elapsed time
is determined by a time-to-digital converter (TDC) - essentially
a stopwatch able to measure time intervals with a resolution of
about 1 ns.
The histogram for that positron detector
is then incremented
in the bin corresponding to the measured time interval.
In most experiments the histogram time range extends up to 5
or 6 muon lifetimes.
The high speed front-end logic of the
data acquisition system, implemented in standard NIM
electronics, is shown schematically in Fig. 2.5.
The rest of the data acquisition electronics
consists of a histogramming memory, various support systems
such as event scalars and detector selection registers
and a computer which controls the experiment and reads
out the data.
Figure 2.5:
Schematic logic diagram of the basic fast front-end electronics
and signal timing for time-differential 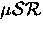 experiments.
Two decay positron detectors are shown; more may be added as
required by the detector geometry.
experiments.
Two decay positron detectors are shown; more may be added as
required by the detector geometry.
 |
In order to measure the elapsed time
we must know from which muon a given decay positron originated.
The easiest way to do this is to veto any event for which
a positron cannot be unambiguously paired with a muon.
Each muon is given a fixed time interval (``pile-up" gate)
to decay, during which the arrival of another muon would veto the
entire sequence and both muons would be discarded.
At meson facilities that produce pions continuously (as opposed to
those with pulsed primary proton beams),
the muons arrive at random time intervals.
This and the dead-time of the TDC place a practical limit
on the mean rate at which one can take muons to about 50,000/s.
Events in which two or more positrons are detected
within the data gate are also rejected by the TDC.
Delays are introduced into the positron ``stop" signals so that
the early part of each histogram contains counts
from uncorrelated start and stop signals.
This allows the background rates to be estimated
from the part of each histogram before t=0, the moment when
start and stop signals happen simultaneously.
Histograms are accumulated for each positron detector i=(B,F,L,R,U,D),
each having the form
| ![\begin{displaymath}
N_i(t) = N_0 \left\{ b_i + {e}^{-t/\tau_{\mu}}[1+ a_i(t)] \right\},\end{displaymath}](img40.gif) |
(5) |
where N0 is the normalization,
ai(t) is the experimental asymmetry
and bi is a time-independent background.
The single-histogram asymmetry is easily obtained from the histogram
by rearranging this;
| ![\begin{displaymath}
a_i(t) = \left[ \frac{N_i(t)}{N_0} - b_i \right] {e}^{t/\tau_{\mu}} -1,\end{displaymath}](img41.gif) |
(6) |
which can be fitted numerically to a model function
to obtain estimates of N0 and bi.
An example of raw histogram data from the Back counter
is shown in Fig. 2.6a.
In this experiment
a transverse magnetic field of 51.5 G caused the muons' spins to precess
at a frequency  =
=  0.699 MHz,
which is apparent in the sinusiodal oscillations in the asymmetry.
Figure 2.6b is the asymmetry
0.699 MHz,
which is apparent in the sinusiodal oscillations in the asymmetry.
Figure 2.6b is the asymmetry  extracted from the raw data using Eq. (2.8);
the solid line is a theoretical asymmetry representing the sum
of two signals with different (exponential) relaxation rates.
extracted from the raw data using Eq. (2.8);
the solid line is a theoretical asymmetry representing the sum
of two signals with different (exponential) relaxation rates.
Figure 2.6:
(a) A histogram from the ``Back" positron detector of a
time-differential experiment on a sample
of liquid Ne.
(b) The asymmetry  extracted from the same histogram
according to Eq. (2.8).
The oscillations are due to the Larmor precession of the muons'
magnetic moments in an externally applied transverse magnetic
field of 51.5 G.
extracted from the same histogram
according to Eq. (2.8).
The oscillations are due to the Larmor precession of the muons'
magnetic moments in an externally applied transverse magnetic
field of 51.5 G.
 |



Next: 2.3 Data Reduction
Up: 2.2 Hardware for Spectroscopy
Previous: 2.2 Hardware for Spectroscopy


![\begin{displaymath}
N_i(t) = N_0 \left\{ b_i + {e}^{-t/\tau_{\mu}}[1+ a_i(t)] \right\},\end{displaymath}](img40.gif)
![\begin{displaymath}
a_i(t) = \left[ \frac{N_i(t)}{N_0} - b_i \right] {e}^{t/\tau_{\mu}} -1,\end{displaymath}](img41.gif)
