5.5 Quadratic Coupling: Two-Phonon Limited Diffusion

The second case we consider has the coupling to lattice excitations taking a form quadratic in atomic displacements so we now write the Hamiltonian, in terms of the same shifted-mode phonon operators as before, as

$${\cal H} = \sum_{\beta} \omega_{\beta} (b_{\beta}^{\dagger} ... ...dagger})(b_{\beta^{\prime}} + b_{-\beta^{\prime}}^{\dagger}).$$ (22)

We continue in the same framework we used in solving the one-phonon problem. Again, we are interested in finding out how much the initial and final states overlap, so we want to construct these states in terms of unitary tranformations of the environmental states. Now the full polaron operator in Eq. (5.24) becomes, with an additional unitary operator for the two-phonon interaction, $\Lambda = \Lambda_1 \Lambda_2$.Again, we write the transition rate, making use of the Fourier transform of the $\delta$-function,

$$W_{12} = \Delta_0^2 \int_{-\infty}^{\infty} dt \, \langle e^... ...{\dagger} \, \Lambda(0) e^{B} \rangle \delta(\xi + E_2 - E_1).$$ (23)

Here $\Lambda_2$ is composed of two parts that arise from the cross terms in the product $(b_{\beta} + b_{-\beta}^{\dagger})(b_{\beta^{\prime}} + b_{-\beta^{\prime}}^{\dagger})$.

There are two kinds (not counting complex conjugates) of two-phonon terms in this; those of the form $b_{\beta} b_{\beta^\prime}$ that create (or annihilate) two separate phonons, and those of the form $b_{\beta}^{\dagger} b_{\beta^{\prime}}$ that annihilate one phonon and create another, therefore allowing scattering of one phonon from one state to another. The largest contribution to the transition rate comes from those terms where the shift of the phonon frequency due to scattering is small; $\omega_{\beta} \approx \omega_{\beta^{\prime}}$.For this reason the scattering part of the two-phonon interaction is said to preserve the phonon population, but strictly speaking it is not precisely unchanged. We are in a regime where coherent (band) diffusion is partially ruined by the scattering of phonons. Further, in the limit of a small shift in phonon frequencies so that $\omega_{\beta} \approx \omega_{\beta^{\prime}}$,we have approximately

$$N_{\beta}(N_{\beta^{\prime}} + 1) \approx \frac{e^{\omega_{\beta}/T}} {(e^{\omega_{\beta}/T} - 1)^2}$$

and we shall see the usual phonon density of states enters as $g^2(\omega)$, not as a density of two-phonon states. Keeping only the scattering terms from Eq. (5.43)

$$\Lambda_{2} \approx \exp \left\{ \sum_{\beta\beta^{\prime}}... ...gger}} {\omega_{\beta} - \omega_{\beta^{\prime}} } \right \}.$$ (24)

We write out the matrix element by the same method as we used for the one-phonon interaction and consider now each mode as separable,

We see that renormalization of the tunnelling bandwidth $\Delta_0$ by the 1-phonon interaction still holds, but now we are also including what will turn out to be a reduction of the effective bandwidth due to the contribution of the two-phonon interaction, corresponding to the terms of the form $b_{\beta}^{\dagger} b_{\beta^{\prime}}$ in $\langle \Lambda_2^{\dagger} \, \Lambda_2 \rangle$.

By the same method as we used earlier, we write out the expectation value in terms of the boson operators

For small frequency shifts $\omega_{\beta} - \omega_{\beta^{\prime}}$this is, to very good approximation,

$$\langle \Lambda_2^{\dagger} \, \Lambda_2 \rangle = \exp \lef... ...{2}(T,\omega)}{2 \pi T} \coth \left( \omega/2T \right) \right\}$$ (25)

with

$$\Omega_{2}(T,\omega) = \pi T \sum_{\beta \beta^{\prime}} \fr... ...me}}) \delta(\omega_{\beta} - \omega_{\beta^{\prime}} - \omega)$$ (26)

We have put $\Omega_{2}(T)$ in this form so we can write

in which we have dropped the time-independent term, since it is small for temperatures low compared to typical 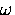$\omega$, and the frequency dependence of $\Omega_2$ since we are in the limit of small differences between phonon frequencies.

The hop rate is then  

$$W_{12}=\Delta_0^2 e^{\xi/2T} \int_{-\infty}^{\infty} e^{i \xi t - \Omega_{2} \vert t\vert}\, dt.$$ (27)

What is the function $\Omega_{2}(T)$? Here it is clear that $\Omega_2$ (which is always a positive, real quantity) takes on the role of an exponential relaxation (or damping) rate of the transition amplitude. The initial and final states during the tunnelling transition have almost exactly the same energy, but phase coherence is lost in the process of scattering phonons. Coherence is suppressed when the transition time $\tau$ is relatively long so that $\Omega_{2} \tau \gt 1$.The integral in Eq. (5.51) converges to

$$W_{12}=\frac{2 \Delta_0^2 \Omega_{2}(T) }{\xi^2 + \Omega_{2}^2(T) }.$$ (28)

The temperature dependence of the hop rate is then determined by the de-coherence rate $\Omega_{2}(T)$ and the interplay with the typical site-to-site energy shift $\xi$. In the following section we will show that $\Omega_{2}(T)$ is a strongly increasing function of temperature and also explore the influence of the phonon density of states on the diffusion rate.