


Next: Analysis
Up: Experiment
Previous: Transverse Field SR
The experiment reported in this thesis used the M20 beamline at TRIUMF
in conjunction with the Helios 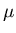 SR spectrometer to study the
LuNi2B2C sample described in Section 3.2. The
M20 beamline delivers muons of mean momentum
SR spectrometer to study the
LuNi2B2C sample described in Section 3.2. The
M20 beamline delivers muons of mean momentum
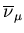 ,
so they stop throughout the bulk of the sample. Figure 4.1
,
so they stop throughout the bulk of the sample. Figure 4.1
![\begin{sidewaysfigure}% latex2html id marker 1625
[tbph]
\begin{center}
\begin{s . . .
. . . d{center}\caption[Experimental setup]{
Experimental setup.}
\end{sidewaysfigure}](img141.gif)
illustrates the path of the muon beam through the experimental
apparatus. The collimator restricts the diameter d of the muon beam
to
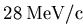 before the beam exits the vacuum of the
beamline through a thin plastic window. Each muon then triggers the muon
counter (M), starting the time to digital converter (TDC).
The muon then travels through two more thin
plastic windows, and the intervening vacuum of a helium gas flow cryostat.
This vacuum thermally insulates the sample space from the warm bore of the
Helios magnet. The muon finally comes to rest in the sample, which is
attached with a little Apiezon N grease to a thin Mylar film stretched over
the end of an aluminium sample holder tube. The crystal
before the beam exits the vacuum of the
beamline through a thin plastic window. Each muon then triggers the muon
counter (M), starting the time to digital converter (TDC).
The muon then travels through two more thin
plastic windows, and the intervening vacuum of a helium gas flow cryostat.
This vacuum thermally insulates the sample space from the warm bore of the
Helios magnet. The muon finally comes to rest in the sample, which is
attached with a little Apiezon N grease to a thin Mylar film stretched over
the end of an aluminium sample holder tube. The crystal
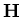 axis
lies parallel to the applied field
H.
An average of
axis
lies parallel to the applied field
H.
An average of
 later the muon decays, emitting a positron
preferentially along the muon spin direction. When this positron is
detected, the TDC is stopped. The TDC therefore records the elapsed time
between the arrival of a muon and the detection of the subsequent decay
positron. Sometimes a muon misses
the sample, and instead it or its decay positron arrives at the veto (V)
counter. Electronic logic modules reject such decay events,
as well as ambiguous ones where the detectors register more than one muon
or more than one positron within specified time periods of
about
later the muon decays, emitting a positron
preferentially along the muon spin direction. When this positron is
detected, the TDC is stopped. The TDC therefore records the elapsed time
between the arrival of a muon and the detection of the subsequent decay
positron. Sometimes a muon misses
the sample, and instead it or its decay positron arrives at the veto (V)
counter. Electronic logic modules reject such decay events,
as well as ambiguous ones where the detectors register more than one muon
or more than one positron within specified time periods of
about
 .
.
Histograms are constructed for the number Ni of positrons
detected in the ith positron counter during each time interval 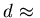 after the TDC starts, from which the muon spin polarisation
P(t) is
computed. Figure 4.2 depicts the arrangement of the positron
after the TDC starts, from which the muon spin polarisation
P(t) is
computed. Figure 4.2 depicts the arrangement of the positron
Figure 4.2:
Cross-sectional view of forward
positron counters Fi and Fij (i = T or B and
j = L or R) as seen by the muon beam (represented as
travelling into the page). The valid detection of a decay positron requires
both the Fi and Fij counters to trigger simultaneously
(
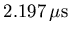 ).
).
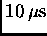 |
detectors. The positron counters form two concentric rings about the muon
beam, with four counters in the inner layer and two in the outer. The inner
detectors cover approximately equal solid angles around the sample, and
the outer counters each completely overlap two of the inner ones. For a
positron detection to be valid, both the inner and outer counters in
a given direction must trigger simultaneously. The appropriate time bin of the
histogram associated with that inner counter then increases by one. The
number Ni of positrons registered per time bin 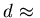 in the
ith inner counter follows the form [7]
in the
ith inner counter follows the form [7]
![\begin{displaymath}
N_i(t) = N_i^0 \exp (-t/ \tau_{\mu})[1 + P_i(t)] + B_i^0
\end{displaymath}](img148.gif) |
(6.3) |
where Ni0 is a normalisation factor and Bi0 is the random background
signal. In the simple situation where all muons experience the same local
field
B, the precession signal Pi(t) recorded by the ith
inner detector is
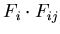 ,
where Ai is
the initial precession amplitude and
,
where Ai is
the initial precession amplitude and  is the initial phase of the
muon spin polarisation
P(0) relative to the centre of the
ith counter. Generally, these precession signals Pi(t) are extracted
numerically from equation (4.3). The single-counter
functions Pi(t) belonging to each pair of opposing inner detectors
combine to produce a component of the complex muon spin polarisation
is the initial phase of the
muon spin polarisation
P(0) relative to the centre of the
ith counter. Generally, these precession signals Pi(t) are extracted
numerically from equation (4.3). The single-counter
functions Pi(t) belonging to each pair of opposing inner detectors
combine to produce a component of the complex muon spin polarisation
 .
Half the difference of the
single-counter functions Pi(t) of an opposing pair constitutes a
polarisation component Px(t) or Py(t), depending on the choice of
detector pair. The complex polarisation
.
Half the difference of the
single-counter functions Pi(t) of an opposing pair constitutes a
polarisation component Px(t) or Py(t), depending on the choice of
detector pair. The complex polarisation
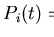 so obtained is then
fitted to a theoretical model to extract the superconducting parameters of
interest. In the experiment reported in this thesis, the four
histograms Ni(t) together typically contained around
so obtained is then
fitted to a theoretical model to extract the superconducting parameters of
interest. In the experiment reported in this thesis, the four
histograms Ni(t) together typically contained around
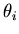 decay
events for a given applied magnetic field H and temperature T,
which were gathered over about two hours.
decay
events for a given applied magnetic field H and temperature T,
which were gathered over about two hours.
Feedback control systems stabilise the applied field H and
temperature T. Current carrying copper coils on the outside of the
Helios superconducting magnet compensate for field drifts detected with
a Hall probe situated near the sample. This keeps external field Hfluctuations below
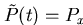 .
Helium streaming past the sample from
the nearby diffuser supplies cooling power, while a Lakeshore 330autotuning temperature controller heats the diffuser.
The heating varies in such a way as to maintain the temperature
of the diffuser at the set value. One calibrated
GaAlAs diode monitors the diffuser temperature,
and two others provide independent readings of the sample temperature.
The analysis of the collected data is explained in the next chapter.
.
Helium streaming past the sample from
the nearby diffuser supplies cooling power, while a Lakeshore 330autotuning temperature controller heats the diffuser.
The heating varies in such a way as to maintain the temperature
of the diffuser at the set value. One calibrated
GaAlAs diode monitors the diffuser temperature,
and two others provide independent readings of the sample temperature.
The analysis of the collected data is explained in the next chapter.



Next: Analysis
Up: Experiment
Previous: Transverse Field SR
Jess H. Brewer
2001-10-31
 later the muon decays, emitting a positron
preferentially along the muon spin direction. When this positron is
detected, the TDC is stopped. The TDC therefore records the elapsed time
between the arrival of a muon and the detection of the subsequent decay
positron. Sometimes a muon misses
the sample, and instead it or its decay positron arrives at the veto (V)
counter. Electronic logic modules reject such decay events,
as well as ambiguous ones where the detectors register more than one muon
or more than one positron within specified time periods of
about
later the muon decays, emitting a positron
preferentially along the muon spin direction. When this positron is
detected, the TDC is stopped. The TDC therefore records the elapsed time
between the arrival of a muon and the detection of the subsequent decay
positron. Sometimes a muon misses
the sample, and instead it or its decay positron arrives at the veto (V)
counter. Electronic logic modules reject such decay events,
as well as ambiguous ones where the detectors register more than one muon
or more than one positron within specified time periods of
about
 .
.
 .
Half the difference of the
single-counter functions Pi(t) of an opposing pair constitutes a
polarisation component Px(t) or Py(t), depending on the choice of
detector pair. The complex polarisation
.
Half the difference of the
single-counter functions Pi(t) of an opposing pair constitutes a
polarisation component Px(t) or Py(t), depending on the choice of
detector pair. The complex polarisation