


Next: Results and Discussion
Up: Analysis
Previous: Calculation of the Core Radius
Fit Quality
Figure 5.5 displays a typical fitted muon precession
signal
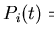 in a rotating reference frame.
in a rotating reference frame.
Figure 5.5:
Fitted muon polarisation
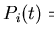 in LuNi2B2C under an applied field
in LuNi2B2C under an applied field
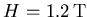 at temperature
at temperature
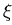 .
The real and imaginary polarisation components are perpendicular to the
field. The squares represent data while the solid lines are the fitted
function (5.1). The insets show the residuals
.
The real and imaginary polarisation components are perpendicular to the
field. The squares represent data while the solid lines are the fitted
function (5.1). The insets show the residuals
 formed
by subtracting the fitted function from the data.
formed
by subtracting the fitted function from the data.
|
The fitted function passes through most of the data points.
The insets to this figure contain residual plots which exhibit
a clear oscillation, indicating that the fitted function
describes the data imperfectly. Such plots offer
a useful qualitative assessment of the accuracy of a fit.
Chi-squared 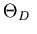 provides a quantitative evaluation of the fit quality.
It is defined as
provides a quantitative evaluation of the fit quality.
It is defined as
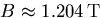 |
(7.8) |
where f(x) is the function fitted to the n measurements
 .
A decrease in
.
A decrease in 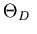 of at least one reveals
a significantly improved fit, while a reduced chi-squared
of at least one reveals
a significantly improved fit, while a reduced chi-squared
 means the fit is perfect. For the results reported in this thesis, the
minimised reduced chi-squareds range between
means the fit is perfect. For the results reported in this thesis, the
minimised reduced chi-squareds range between
 and
and
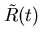 .
These fits are comparable in quality to those obtained
for other superconductors through analysis of
.
These fits are comparable in quality to those obtained
for other superconductors through analysis of 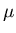 SR data in the time domain.
Use of a more accurate cutoff factor [50]
than the simple Gaussian
SR data in the time domain.
Use of a more accurate cutoff factor [50]
than the simple Gaussian
 in expression (5.2)
might supply better fits for the LuNi2B2C data discussed in this thesis.
Figure 5.6 shows the dependence of
in expression (5.2)
might supply better fits for the LuNi2B2C data discussed in this thesis.
Figure 5.6 shows the dependence of 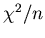 on the penetration
depth
on the penetration
depth 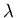 in LuNi2B2C at several temperatures T, and Table 5.1
lists the number of degrees of freedom n for each of these temperatures.
(The number of degrees of freedom n for fits at other temperatures is
similar.)
in LuNi2B2C at several temperatures T, and Table 5.1
lists the number of degrees of freedom n for each of these temperatures.
(The number of degrees of freedom n for fits at other temperatures is
similar.)
![\begin{sidewaysfigure}% latex2html id marker 2073
[tbph]
\begin{center}
\begin{s . . .
. . . e for each temperature~$T$ appears in Table~\ref{tab:ndf}.}
\end{sidewaysfigure}](img201.gif)
Table 5.1:
Number of data points n analysed at each temperature T
in Figures 5.6, 5.7 and 5.8.
| Temperature T (
K) |
Number of data points n |
| 2.6 |
556 |
| 5.5 |
550 |
| 8.5 |
547 |
For each set value of the penetration depth 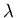 the parameters vary,
in the way described in Section 5.3, until
the parameters vary,
in the way described in Section 5.3, until 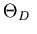 is minimised. The error bars for fitted parameters reported
in this thesis are the amount by which the parameter must change to
raise
is minimised. The error bars for fitted parameters reported
in this thesis are the amount by which the parameter must change to
raise 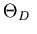 by one while the other parameters vary normally.
At each temperature there is a clear minimum in
by one while the other parameters vary normally.
At each temperature there is a clear minimum in 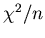 as a
function of penetration depth
as a
function of penetration depth 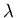 ,
which
moves to higher values of the penetration depth
,
which
moves to higher values of the penetration depth 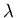 at warmer
temperatures. The shallowness of the minima is at least partly a
consequence of compensation by the other free parameters, especially the
nonlocality
parameter C. Parameter C drops monotonically by two to three orders of
magnitude over the displayed interval of increasing penetration depth
at warmer
temperatures. The shallowness of the minima is at least partly a
consequence of compensation by the other free parameters, especially the
nonlocality
parameter C. Parameter C drops monotonically by two to three orders of
magnitude over the displayed interval of increasing penetration depth 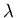 .
This substantial playoff comes from the factor
.
This substantial playoff comes from the factor
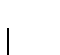 appearing in
the internal spatial field profile (5.2). The widening minima at
higher temperatures T reflects the diminishing asymmetry of the internal field
distribution n(B) as it approaches a Gaussian form. Figure 5.7
reveals how
appearing in
the internal spatial field profile (5.2). The widening minima at
higher temperatures T reflects the diminishing asymmetry of the internal field
distribution n(B) as it approaches a Gaussian form. Figure 5.7
reveals how 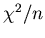 varies with the nonlocality parameter C.
varies with the nonlocality parameter C.
![\begin{sidewaysfigure}% latex2html id marker 2101
[tbph]
\begin{center}
\begin{s . . .
. . . each temperature~$T$\space appears in Table~\ref{tab:ndf}.}
\end{sidewaysfigure}](img203.gif)
At each temperature 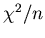 grows rapidly as Cdecreases below the location of the minimum
grows rapidly as Cdecreases below the location of the minimum 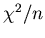 .
This clearly
demonstrates the substantial improvement in fit quality achieved by
incorporating nonlocal corrections into the London model. The slow growth
in
.
This clearly
demonstrates the substantial improvement in fit quality achieved by
incorporating nonlocal corrections into the London model. The slow growth
in 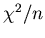 as the nonlocality parameter C increases away from the
minimum further evidences the playoff between C and the
penetration depth
as the nonlocality parameter C increases away from the
minimum further evidences the playoff between C and the
penetration depth 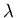 .
The penetration depth
.
The penetration depth 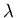 falls
monotonically as the nonlocality parameter C rises
over the plotted interval. The shallower minima at warmer temperatures Tagain stem from the more Gaussian-like internal field distribution n(B).
Figure 5.8 displays
falls
monotonically as the nonlocality parameter C rises
over the plotted interval. The shallower minima at warmer temperatures Tagain stem from the more Gaussian-like internal field distribution n(B).
Figure 5.8 displays 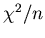 for a
range of vortex core radii
for a
range of vortex core radii 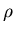 at the same temperatures T.
at the same temperatures T.
![\begin{sidewaysfigure}% latex2html id marker 2115
[tbph]
\begin{center}
\begin{s . . .
. . . e for each temperature~$T$ appears in Table~\ref{tab:ndf}.}
\end{sidewaysfigure}](img204.gif)
Since the core radius 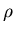 is a calculated rather than fitted parameter,
this graph is constructed by minimising
is a calculated rather than fitted parameter,
this graph is constructed by minimising 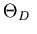 at fixed values of
the coherence length
at fixed values of
the coherence length 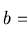 and noting the corresponding core radii
and noting the corresponding core radii 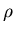 .
The
strongly linear relationship between the coherence length
.
The
strongly linear relationship between the coherence length 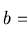 and the
core radius
and the
core radius 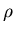 makes this process possible. Similarly, altering the
coherence length
makes this process possible. Similarly, altering the
coherence length 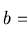 by its uncertainty
by its uncertainty 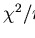 and observing the
consequent change in the core radius
and observing the
consequent change in the core radius 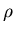 produces error bars
produces error bars
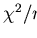 for the
core radius
for the
core radius 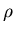 .
This means of computation of the uncertainty
.
This means of computation of the uncertainty
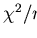 in the core radius
in the core radius 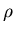 is far simpler and more tractable than one based
on combining the uncertainties of the fitted parameters according to
equations (5.2) and (5.10).
At each temperature T the
is far simpler and more tractable than one based
on combining the uncertainties of the fitted parameters according to
equations (5.2) and (5.10).
At each temperature T the 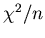 curve
has a single minimum, which moves to larger core radii
curve
has a single minimum, which moves to larger core radii 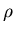 as the
temperature T rises. This behaviour of the core radius
as the
temperature T rises. This behaviour of the core radius 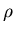 ,
and also the
penetration depth
,
and also the
penetration depth  ,
with temperature T is explored in more detail in
the next chapter.
,
with temperature T is explored in more detail in
the next chapter.



Next: Results and Discussion
Up: Analysis
Previous: Calculation of the Core Radius
Jess H. Brewer
2001-10-31
![]() in a rotating reference frame.
in a rotating reference frame.
![]() provides a quantitative evaluation of the fit quality.
It is defined as
provides a quantitative evaluation of the fit quality.
It is defined as
 .
A decrease in
.
A decrease in  means the fit is perfect. For the results reported in this thesis, the
minimised reduced chi-squareds range between
means the fit is perfect. For the results reported in this thesis, the
minimised reduced chi-squareds range between
 and
and
 in expression (5.2)
might supply better fits for the LuNi2B2C data discussed in this thesis.
Figure 5.6 shows the dependence of
in expression (5.2)
might supply better fits for the LuNi2B2C data discussed in this thesis.
Figure 5.6 shows the dependence of ![\begin{sidewaysfigure}% latex2html id marker 2073
[tbph]
\begin{center}
\begin{s . . .
. . . e for each temperature~$T$ appears in Table~\ref{tab:ndf}.}
\end{sidewaysfigure}](img201.gif)
 appearing in
the internal spatial field profile (5.2). The widening minima at
higher temperatures T reflects the diminishing asymmetry of the internal field
distribution n(B) as it approaches a Gaussian form. Figure 5.7
reveals how
appearing in
the internal spatial field profile (5.2). The widening minima at
higher temperatures T reflects the diminishing asymmetry of the internal field
distribution n(B) as it approaches a Gaussian form. Figure 5.7
reveals how