


Next: BCS Theory
Up: Superconductivity
Previous: Superconductivity
London Theory
The London equations [8] deal with the electrodynamic behaviour of
superconductors on a macroscopic scale. They relate the local
electric (
E) and magnetic (
B) fields to the
supercurrent density
J as
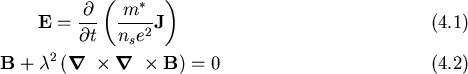
The supercurrent density
J is due to the number density ns of
carriers (either electrons or holes, depending on the superconductor) of
effective mass m* which encounter no resistance. The London
penetration depth, defined as
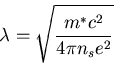 |
(4.1) |
is the only free parameter in these equations.
The first London equation (2.1) expresses perfect
conductivity in that the electric field accelerates the superelectrons.
The second equation describes the Meissner effect. It implies that
within a superconductor an external magnetic field decays over
the characteristic distance 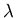 .
An example of this is the situation
illustrated in Figure 2.1, where a constant applied field
.
An example of this is the situation
illustrated in Figure 2.1, where a constant applied field
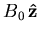 exists parallel to the surface at x = 0 of a superconductor.
exists parallel to the surface at x = 0 of a superconductor.
![\begin{sidewaysfigure}% latex2html id marker 384
[tbph]
\begin{center}
\begin{si . . .
. . . terises the distance over which
an applied field decays.
}
\end{sidewaysfigure}](img22.gif)
With the aid of the vector identity
and one of Maxwell's equations,
 ,
equation (2.2) becomes
,
equation (2.2) becomes
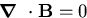 |
(4.3) |
Inside the superconductor the solution for the internal field B is then
 ,
as plotted in Figure 2.1. With slight modification these London
equations continue to be valid in the presence of magnetic vortices.
,
as plotted in Figure 2.1. With slight modification these London
equations continue to be valid in the presence of magnetic vortices.
The spatial magnetic field profile of a vortex lattice can be modelled with
a generalized London theory. For an array of flux lines at positions
ri, expression (2.2) becomes [9]
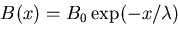 |
(4.4) |
This equation portrays each filament of one flux quantum  as having the proportions of a two-dimensional delta function, leading to
unrealistic field and supercurrent divergences at the vortex centre.
Such unphysical behaviour disappears through the incorporation of
finite core size, often achieved by multiplying Fourier
components of the field B with a cutoff factor in reciprocal space.
Equation (2.6) applies when
the external field H lies far enough from the upper critical field Hc2that the vortices are substantially more than the radius of a physical
vortex apart. The internal field then consists of the superposition of
the contributions [9]
as having the proportions of a two-dimensional delta function, leading to
unrealistic field and supercurrent divergences at the vortex centre.
Such unphysical behaviour disappears through the incorporation of
finite core size, often achieved by multiplying Fourier
components of the field B with a cutoff factor in reciprocal space.
Equation (2.6) applies when
the external field H lies far enough from the upper critical field Hc2that the vortices are substantially more than the radius of a physical
vortex apart. The internal field then consists of the superposition of
the contributions [9]
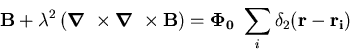 |
(4.5) |
from each flux line i, where  is the Hankel
function of imaginary argument of zero order. An explanation of the flux
line lattice geometry transitions induced by external field changes in
superconductors like LuNi2B2C demands a further extension of the London
equations [10][11].
is the Hankel
function of imaginary argument of zero order. An explanation of the flux
line lattice geometry transitions induced by external field changes in
superconductors like LuNi2B2C demands a further extension of the London
equations [10][11].
Nonlocal electrodynamics accounts for the dependence of the supercurrent
density
J(r) on the vector potential
A(r) within a characteristic range 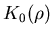 from the
point
r [12]. The effects of nonlocality are
significant in regions where the vector potential
A(r)varies rapidly within a volume of
radius
from the
point
r [12]. The effects of nonlocality are
significant in regions where the vector potential
A(r)varies rapidly within a volume of
radius
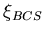 [8][13],
provided that the temperature is low and the mean
free path l exceeds this radius. Otherwise scattering suppresses nonlocal
effects [12]. The basic London equations (2.1)
and (2.2) derive from the local relation
[8][13],
provided that the temperature is low and the mean
free path l exceeds this radius. Otherwise scattering suppresses nonlocal
effects [12]. The basic London equations (2.1)
and (2.2) derive from the local relation
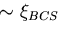 |
(4.6) |
by taking the time derivative and the curl respectively [8] or,
in terms of spatial Fourier components [13],
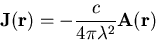 |
(4.7) |
Inclusion of nonlocality transforms this equation to [12]
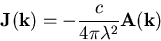 |
(4.8) |
where the expression for the kernel
Q(k) emerges from the
microscopic approach of the Bardeen-Cooper-Schrieffer (BCS) theory.



Next: BCS Theory
Up: Superconductivity
Previous: Superconductivity
Jess H. Brewer
2001-10-31
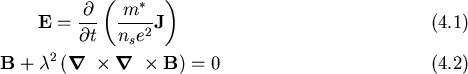
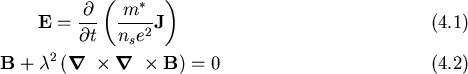
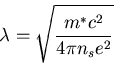
![\begin{sidewaysfigure}% latex2html id marker 384
[tbph]
\begin{center}
\begin{si . . .
. . . terises the distance over which
an applied field decays.
}
\end{sidewaysfigure}](img22.gif)
 ,
equation (2.2) becomes
,
equation (2.2) becomes
 ,
as plotted in Figure 2.1. With slight modification these London
equations continue to be valid in the presence of magnetic vortices.
,
as plotted in Figure 2.1. With slight modification these London
equations continue to be valid in the presence of magnetic vortices.
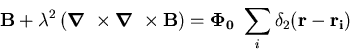
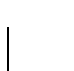 is the Hankel
function of imaginary argument of zero order. An explanation of the flux
line lattice geometry transitions induced by external field changes in
superconductors like LuNi2B2C demands a further extension of the London
equations [10][11].
is the Hankel
function of imaginary argument of zero order. An explanation of the flux
line lattice geometry transitions induced by external field changes in
superconductors like LuNi2B2C demands a further extension of the London
equations [10][11].
![]() from the
point
r [12]. The effects of nonlocality are
significant in regions where the vector potential
A(r)varies rapidly within a volume of
radius
from the
point
r [12]. The effects of nonlocality are
significant in regions where the vector potential
A(r)varies rapidly within a volume of
radius
![]() [8][13],
provided that the temperature is low and the mean
free path l exceeds this radius. Otherwise scattering suppresses nonlocal
effects [12]. The basic London equations (2.1)
and (2.2) derive from the local relation
[8][13],
provided that the temperature is low and the mean
free path l exceeds this radius. Otherwise scattering suppresses nonlocal
effects [12]. The basic London equations (2.1)
and (2.2) derive from the local relation