


Up: J.E. Sonier's M.Sc. Thesis
Previous: Bibliography
The computer time allocated to calculating
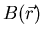 of Eq. (3.9), is significant enough that it is
practical to avoid the large sum over reciprocal lattice vectors
of Eq. (3.9), is significant enough that it is
practical to avoid the large sum over reciprocal lattice vectors
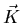 for each iteration in the
for each iteration in the 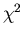 -minimization
procedure. Consequently, a Taylor series expansion around an initial
value of the magnetic penetration depth
-minimization
procedure. Consequently, a Taylor series expansion around an initial
value of the magnetic penetration depth
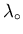 was employed in the actual
fitting program:
was employed in the actual
fitting program:
so that,
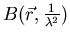 is determined by expanding about the initial
point
is determined by expanding about the initial
point
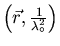 .
In this way,
.
In this way,
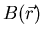 is calculated
by summing over the reciprocal lattice vectors
is calculated
by summing over the reciprocal lattice vectors 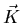 [in Eq. (3.9)], only once for an initial set of parameters
[in Eq. (3.9)], only once for an initial set of parameters
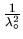 and
and 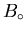 ,
where
,
where 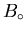 is the initial value of the
average field. It is not necessary to expand about
is the initial value of the
average field. It is not necessary to expand about 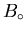 .
This
is because changes in the average field merely shift the field distribution
along the field (or frequency) axis. In the fitting process, field shifts
in excess of a conservative value of
.
This
is because changes in the average field merely shift the field distribution
along the field (or frequency) axis. In the fitting process, field shifts
in excess of a conservative value of
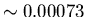 T were not permitted
before the program was stopped, the initial parameters changed, and the
data refitted.
T were not permitted
before the program was stopped, the initial parameters changed, and the
data refitted.
Table A.1:
Accuracy of the Taylor series expansion used in the fitting program.
| |
|
|
|
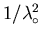 |
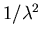 |
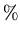 Error in
Error in |
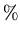 Error in
Error in |
| |
|
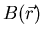 at the
at the |
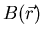 at the
at the |
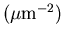 |
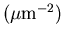 |
vortex core. |
saddle point. |
| |
|
|
|
| |
|
|
|
| 50 |
50 |
0.00 |
0.00 |
| 50 |
49 |
0.16 |
0.14 |
| 50 |
48 |
0.31 |
0.27 |
| 50 |
47 |
0.47 |
0.40 |
| 50 |
46 |
0.62 |
0.53 |
| 50 |
45 |
0.78 |
0.67 |
| 50 |
44 |
0.93 |
0.80 |
| 50 |
43 |
1.08 |
0.93 |
| 50 |
30 |
3.01 |
2.65 |
| 50 |
20 |
4.43 |
3.96 |
| 50 |
10 |
5.78 |
5.25 |
| 50 |
0 |
7.07 |
6.54 |
| |
|
|
|
|
Table A.1
shows the accuracy of the Taylor series assuming an average magnetic
field 0.5T and
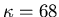 .
The error in using Eq. (A.1),
expressed as a percentage of
the exact calculation of
.
The error in using Eq. (A.1),
expressed as a percentage of
the exact calculation of
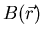 using
Eq. (3.9), is shown for
using
Eq. (3.9), is shown for
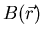 calculated at the
vortex core and at a saddle point. The results show that even
large changes in
calculated at the
vortex core and at a saddle point. The results show that even
large changes in
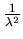 give a good approximation for
give a good approximation for
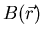 .
In a typical fit,
.
In a typical fit,
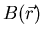 is calculated in excess of 150,000times, so that using a Taylor series greatly diminishes the time required to
fit.
is calculated in excess of 150,000times, so that using a Taylor series greatly diminishes the time required to
fit.



Up: J.E. Sonier's M.Sc. Thesis
Previous: Bibliography
Jess H. Brewer
2001-09-28
![]() of Eq. (3.9), is significant enough that it is
practical to avoid the large sum over reciprocal lattice vectors
of Eq. (3.9), is significant enough that it is
practical to avoid the large sum over reciprocal lattice vectors
![]() for each iteration in the
for each iteration in the ![]() -minimization
procedure. Consequently, a Taylor series expansion around an initial
value of the magnetic penetration depth
-minimization
procedure. Consequently, a Taylor series expansion around an initial
value of the magnetic penetration depth
![]() was employed in the actual
fitting program:
was employed in the actual
fitting program:
![]() .
The error in using Eq. (A.1),
expressed as a percentage of
the exact calculation of
.
The error in using Eq. (A.1),
expressed as a percentage of
the exact calculation of
![]() using
Eq. (3.9), is shown for
using
Eq. (3.9), is shown for
![]() calculated at the
vortex core and at a saddle point. The results show that even
large changes in
calculated at the
vortex core and at a saddle point. The results show that even
large changes in
![]() give a good approximation for
give a good approximation for
![]() .
In a typical fit,
.
In a typical fit,
![]() is calculated in excess of 150,000times, so that using a Taylor series greatly diminishes the time required to
fit.
is calculated in excess of 150,000times, so that using a Taylor series greatly diminishes the time required to
fit.