 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE
First, what is a charge? We don't know!
But then, we don't know what a mass is, either,
except in terms of its behaviour: a mass resists acceleration
by forces and attracts other masses with a gravitational force.
The analogy is apt, in the sense that electrical charges exert
forces on each other in almost exactly the same way as masses do,
except for two minor differences, which I will come to shortly.
Recall Newton's UNIVERSAL LAW OF GRAVITATION in its most
democratic form: the force
![]() acting on
body #2 (mass m2) due to body #1 (mass m1) is
acting on
body #2 (mass m2) due to body #1 (mass m1) is
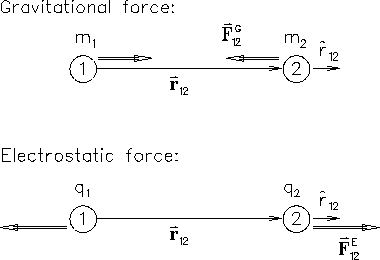 |
So what are the "minor differences?"
Well, the first one is in the sign.
Both "coupling constants" (G and kE)
are defined to be positive; therefore the - sign
in the first equation tells us that the gravitational force
![]() on mass #2 is in the opposite direction
from the unit vector
on mass #2 is in the opposite direction
from the unit vector
![]() pointing form #1 to #2
-- i.e. the force is attractive, back toward the other body.
All masses attract all other masses gravitationally;
there are (so far as we know) no repulsive forces in gravity.
Another way of putting it would be to say that
"there are no negative masses."
By contrast, electric charges come in
both positive (+) and negative (-) varieties; moreover,
Eq. (1) tells us that the electrical force
pointing form #1 to #2
-- i.e. the force is attractive, back toward the other body.
All masses attract all other masses gravitationally;
there are (so far as we know) no repulsive forces in gravity.
Another way of putting it would be to say that
"there are no negative masses."
By contrast, electric charges come in
both positive (+) and negative (-) varieties; moreover,
Eq. (1) tells us that the electrical force
![]() on charge #2 is in the same direction
as
on charge #2 is in the same direction
as
![]() as long as the product q1 q2 is positive - i.e.
as long as the product q1 q2 is positive - i.e.
charges of like sign [both + or both -] repel
whereas unlike charges attract.
The second "minor difference" between electrical
and gravitational forces is in their magnitudes.
Of course, each depends on the size of
the "coupling constant"
[G for gravity vs. kE for electrostatics]
as well as the sizes of the "sources"
[m1 and m2 for gravity vs. q1 and q2 for electrostatics]
so any discussion of magnitude has to be in reference to
"typical" examples. Let's choose the heaviest stable
elementary particle that has both charge and mass:
the proton, which constitutes the nucleus of a
hydrogen atom.17.3
A proton has a positive charge of