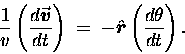BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Next: Kepler
Up: Circular Motion
Previous: Rate of Change of a Vector
Figure:
Differences between vectors at slightly different times
for a body in uniform circular motion.
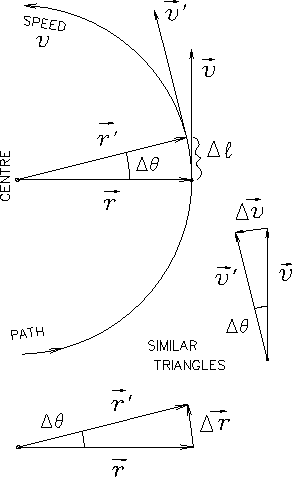 |
From Fig. 10.3 we can see the relationship between
the change in position
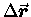 and the change in velocity
and the change in velocity
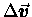 in a short time interval
in a short time interval 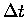 .
As all three get smaller and smaller,
.
As all three get smaller and smaller,
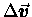 gets to be more and more exactly in the centripetal direction
(along
gets to be more and more exactly in the centripetal direction
(along
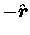 )
and its scalar magnitude
)
and its scalar magnitude 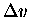 will always (from similar triangles) be given by
will always (from similar triangles) be given by
where I have been careful to write
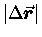 rather than
rather than 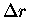 since the magnitude of the
radius vector, r, does not change!
Now is a good time to note that, for a tiny sliver of a circle,
there is a vanishingly small difference between
since the magnitude of the
radius vector, r, does not change!
Now is a good time to note that, for a tiny sliver of a circle,
there is a vanishingly small difference between
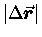 and the actual distance
and the actual distance
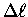 travelled along the arc, which is given exactly by
travelled along the arc, which is given exactly by
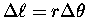 .
Thus
.
Thus
If we divide both sides by 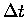 and then take the limit
as
and then take the limit
as
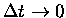 ,
the approximation becomes arbitrarily good
and we get
,
the approximation becomes arbitrarily good
and we get
We can now combine this with the definitions of acceleration
(
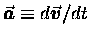 )
and angular velocity
(
)
and angular velocity
(
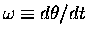 )
to give
(after multiplying both sides by v)
)
to give
(after multiplying both sides by v)
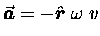 .
We need only divide the equation
.
We need only divide the equation
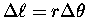 by
by 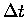 and let
and let
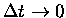 to realize that
to realize that
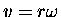 .
If we substitute this result into our equation
for the acceleration, it becomes
.
If we substitute this result into our equation
for the acceleration, it becomes
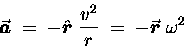 |
(10.2) |
which is our familiar result for the centripetal acceleration
in explicitly vectorial form.


Next: Kepler
Up: Circular Motion
Previous: Rate of Change of a Vector
Jess H. Brewer -
Last modified: Sat Nov 14 12:24:50 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE 
![]() and the change in velocity
and the change in velocity
![]() in a short time interval
in a short time interval ![]() .
As all three get smaller and smaller,
.
As all three get smaller and smaller,
![]() gets to be more and more exactly in the centripetal direction
(along
gets to be more and more exactly in the centripetal direction
(along
![]() )
and its scalar magnitude
)
and its scalar magnitude ![]() will always (from similar triangles) be given by
will always (from similar triangles) be given by