BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Next: The Bohr Radius
Up: Particle in a Box
Previous: A 1-Dimensional Box
If the electron travels in a circular path
(as postulated by Niels Bohr in 1913) then
we must apply de Broglie's hypothesis in a slightly different way:
namely, the electron's "wave" must be single valued
-- it has to get back to the same value as it travels
around the closed loop back to where it started.
This means that the circumference of the loop is an
integer number of wavelengths, or
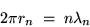 |
(24.7) |
where rn is the radius of the orbit for the
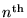 allowed mode.
This in turn predicts a relationship between the radius and the momentum,
allowed mode.
This in turn predicts a relationship between the radius and the momentum,
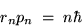 |
(24.8) |
where
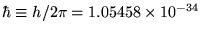 J-s.
[Actually in any sensible system of units
J-s.
[Actually in any sensible system of units 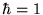 ,
just like c = 1, but we are forced by tyrannical
bureaucrats and twisted social conventions to use SI units.]
,
just like c = 1, but we are forced by tyrannical
bureaucrats and twisted social conventions to use SI units.]
But what is the product of the radius and the momentum
for a circular orbit? The ANGULAR MOMENTUM!
Thus Voila! We have Bohr's hypothesis,
namely that angular momentum L is quantized in units of 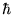 :
:
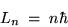 |
(24.9) |


Next: The Bohr Radius
Up: Particle in a Box
Previous: A 1-Dimensional Box
Jess H. Brewer -
Last modified: Wed Nov 18 17:28:49 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE ![]() :
: