BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Next: Sinusoidal Motion
Up: Simple Harmonic Motion
Previous: Simple Harmonic Motion
Nature shows us many "systems" which return periodically
to the same initial state, passing through the same sequence
of intermediate states every period. Life is so full of
periodic experiences, from night and day
to the rise and fall of the tides
to the phases of the moon
to the annual cycle of the seasons,
that we all come well equipped with "common sense"
tailored to this paradigm.13.1
It has even been suggested
that the concept of time itself is rooted in
the cyclic phenomena of Nature.
In Physics, of course, we insist on narrowing the definition
just enough to allow precision. For instance, many phenomena
are cyclic without being periodic in the strict
sense of the word.13.2
Here cyclic means that the same
general pattern keeps repeating; periodic means that
the system passes through the same "phase" at exactly
the same time in every cycle and that all the cycles are
exactly the same length. Thus if we know all the
details of one full cycle of true periodic behaviour,
then we know the subsequent state of the system at all times,
future and past. Naturally, this is an idealization;
but its utility is obvious.
Figure:
Some periodic functions.
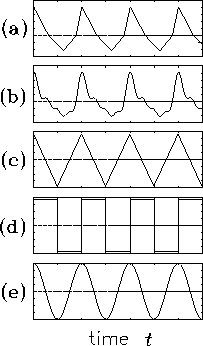
Of course, there is an infinite variety of possible periodic
cycles. Assuming that we can reduce the "state" of the system
to a single variable "q" and its time derivatives, the graph
of q(t) can have any shape as long as it repeats
after one full period. Fig. 13.1 illustrates
a few examples. In (a) and (b) the "displacement" of q
away from its "equilibrium" position [dashed line] is not
symmetric, yet the phases repeat every cycle. In (c) and (d)
the cycle is symmetric with the same "amplitude" above and below
the equilibrium axis, but at certain points the slope of the
curve changes "discontinuously." Only in (e) is the cycle
everywhere smooth and symmetric.


Next: Sinusoidal Motion
Up: Simple Harmonic Motion
Previous: Simple Harmonic Motion
Jess H. Brewer -
Last modified: Sun Nov 15 13:33:31 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE