BELIEVE   ME   NOT!    - -     A   SKEPTIC's   GUIDE  

Conditional Multiplicity

Suppose we have a jar full of pennies, say  N  pennies, all of which have had unique numbers painted on them so that they can be easily distinguished from each other. Now suppose we shake it thoroughly and dump it out on a nice flat table; each penny falls either "heads" or "tails" with equal a priori probability. The probability of penny #1 being "heads" is $\onehalf$. The probability of penny #1 being "heads" and penny #2 being "tails" is $\onehalf \times \onehalf = \onefourth$. The probability of penny #1 being "heads" and penny #2 being "tails" and penny #3 being "tails" is $\onehalf \times \onehalf \times \onehalf = {1 \over 8}$. And so on. If the pennies are all "statistically independent" (i.e. how one penny falls has no influence on the other pennies), the probability of any specific arrangement of specific pennies falling specific ways [what we call a fully specified state of the system] is

$$\left( 1 \over 2 \right)^N \; = \; {1 \over 2^N}$$

where  N  is the total number of pennies.

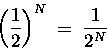
Unfortunately, this is not what we want to know. We don't care which pennies fall which way,^15.2 only how many of each. This is what we call a partially specified or partially constrained state of the system. What we really want to know is the number of ways we can get  n  heads and  (N-n)  tails.^15.3

Suppose we specify that  n  pennies are "heads" and the remaining  (N-n)  are "tails." The number of ways we can do this is what we call   $\Omega(n,N)$,  the multiplicity function for the partially constrained state specified only by  n  and  N. Here's how we calculate   $\Omega(n,N)$:  the number of different ways we can rearrange all  N  coins is

$$N! \equiv N \cdot (N-1) \cdot (N-2) \cdots 3 \cdot 2 \cdot 1$$

because we have  N  choices of which coin will be first, then we have  (N-1)  choices of which coin will be second, then we have  (N-2)  choices of which coin will be third, and so on. The total number of choices is the product of the numbers of choices at each step. However, we have overcounted by the number of different ways the heads can be rearranged among themselves, which by the same argument is  n!,  and by the number  (N-n)!  of ways the tails can be rearranged among themselves. Therefore the total number of distinguishable combinations that all give  n  heads and  (N-n)  tails is

$$\Omega(n,N) = { N! \over n! \, \cdot \, (N-n)! }$$ (15.1)

Another example would be a parking lot with  N  spaces in which  n  cars are parked. The number of different ways we can label the spaces is  N!  but the  n  occupied spaces can be rearranged amongst themselves  n!  different ways and the  (N-n)  empty spaces can be rearranged  (N-n)!  different ways without altering the partial constraint [namely, that only  n  of the spaces are filled].^15.4 Then Eq. (1) describes the number of different ways the cars can be parked without changing the total number of parked cars.