


Next: The Mass of
Up: No Title
Previous: Conversion of Energy
In the previous handout we encountered the notion of
4-vectors, the prototype of which is the space-time
vector, 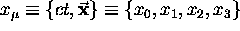 ,
where the ``zeroth component''
,
where the ``zeroth component'' 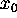 is time
multiplied by the speed of light:
is time
multiplied by the speed of light: 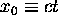 and
the remaining three components are the three ordinary
spatial coordinates. [The notation is new but the idea is the same.]
In general we assume that a vector with Greek indices
(like
and
the remaining three components are the three ordinary
spatial coordinates. [The notation is new but the idea is the same.]
In general we assume that a vector with Greek indices
(like 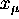 ) is a 4-vector, while a vector with
Roman indices (like
) is a 4-vector, while a vector with
Roman indices (like 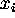 ) is an ordinary spatial 3-vector.
) is an ordinary spatial 3-vector.
It can be shown
 that the inner or scalar product of any two
4-vectors has the agreeable property of being
a Lorentz invariant - i.e. it is unchanged by
a Lorentz transformation - i.e. it has the
same value for all observers. This comes in
very handy in the confusing world of Relativity!
We write the scalar product of two 4-vectors
as follows:
that the inner or scalar product of any two
4-vectors has the agreeable property of being
a Lorentz invariant - i.e. it is unchanged by
a Lorentz transformation - i.e. it has the
same value for all observers. This comes in
very handy in the confusing world of Relativity!
We write the scalar product of two 4-vectors
as follows:
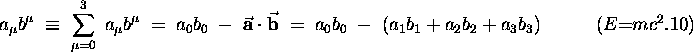
where the first equivalence expresses the
Einstein summation convention - we automatically
sum over repeated indices. Note the - sign!
It is part of the definition of the ``metric'' of
space and time, just like the Pythagorean theorem
defines the ``metric'' of flat 3-space in Euclidean geometry.
Our first Lorentz invariant was the proper time
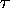 of an event, which is just the square root
of the scalar product of the space-time 4-vector
with itself:
of an event, which is just the square root
of the scalar product of the space-time 4-vector
with itself:
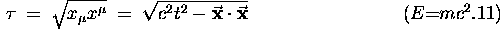
We now encounter our second 4-vector, and probably
the last one we need for our purposes here;
the energy-momentum 4-vector,
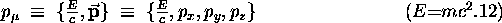
where 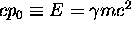 is the total relativistic energy
and
is the total relativistic energy
and  is the usual momentum 3-vector
of some object in whose kinematics we are interested.
[Check for yourself that all the components of this vector
have the same units, as required.]
If we take the scalar product of
is the usual momentum 3-vector
of some object in whose kinematics we are interested.
[Check for yourself that all the components of this vector
have the same units, as required.]
If we take the scalar product of 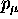 with itself,
we get a new Lorentz invariant:
with itself,
we get a new Lorentz invariant:
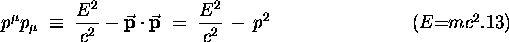
where 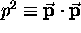 is the square
of the magnitude of the ordinary 3-vector momentum.
is the square
of the magnitude of the ordinary 3-vector momentum.
It turns out that the constant value of this particular Lorentz invariant
is just the
that the constant value of this particular Lorentz invariant
is just the 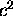 times the square of the rest mass
of the object whose momentum we are scrutinizing:
times the square of the rest mass
of the object whose momentum we are scrutinizing:
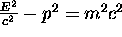 or
or 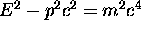 .
As a result, we can write
.
As a result, we can write

which is a very useful formula relating the
energy E, the rest mass m
and the momentum p of a relativistic body.
Although there are lots of other Lorentz invariants
we can define by taking the scalar products of 4-vectors,
these two will suffice for my purposes; you may forget this
derivation entirely if you so choose, but I will need
Eq. (E=mc2.14)
for future reference.



Next: The Mass of
Up: No Title
Previous: Conversion of Energy
Jess Brewer
Fri Sep 13 11:17:01 PDT 1996
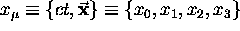 ,
where the ``zeroth component''
,
where the ``zeroth component'' 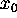 is time
multiplied by the speed of light:
is time
multiplied by the speed of light: 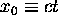 and
the remaining three components are the three ordinary
spatial coordinates. [The notation is new but the idea is the same.]
In general we assume that a vector with Greek indices
(like
and
the remaining three components are the three ordinary
spatial coordinates. [The notation is new but the idea is the same.]
In general we assume that a vector with Greek indices
(like 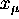 ) is a 4-vector, while a vector with
Roman indices (like
) is a 4-vector, while a vector with
Roman indices (like 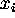 ) is an ordinary spatial 3-vector.
) is an ordinary spatial 3-vector.
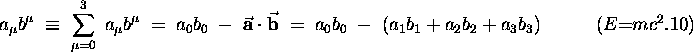
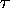 of an event, which is just the square root
of the scalar product of the space-time 4-vector
with itself:
of an event, which is just the square root
of the scalar product of the space-time 4-vector
with itself:
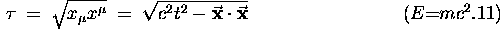
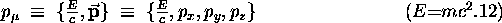
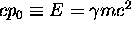 is the total relativistic energy
and
is the total relativistic energy
and  is the usual momentum 3-vector
of some object in whose kinematics we are interested.
[Check for yourself that all the components of this vector
have the same units, as required.]
If we take the scalar product of
is the usual momentum 3-vector
of some object in whose kinematics we are interested.
[Check for yourself that all the components of this vector
have the same units, as required.]
If we take the scalar product of 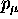 with itself,
we get a new Lorentz invariant:
with itself,
we get a new Lorentz invariant:
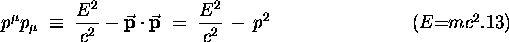
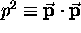 is the square
of the magnitude of the ordinary 3-vector momentum.
is the square
of the magnitude of the ordinary 3-vector momentum.
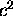 times the square of the rest mass
of the object whose momentum we are scrutinizing:
times the square of the rest mass
of the object whose momentum we are scrutinizing:
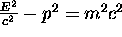 or
or 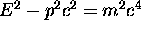 .
As a result, we can write
.
As a result, we can write
