3.3 A minor correction to the Lorentzian theory

 In the previous section, the Lorentzian theory was introduced as a muon spin relaxation theory for dilute spin systems. This theory is based on the Lorentzian field distribution at the muon sites. Still, a truly Lorentzian distribution is unphysical, because some fraction of the muons must locate at an infinitesimally small distance from a magnetic ion, in order to realize the diverging second moment of the Lorentzian distribution $<H_{\rm loc}^2\gt-<H_{\rm loc}\gt^2\rightarrow\infty$. To restore the physicality of the local field distribution, it will be natural to introduce a large cut-off field ($\Delta_{\rm max}$) to the Lorentzian distribution. This idea is easily formulated in the Gaussian decomposed picture of the Lorentzian distribution (eq.29,30), which has been introduced to obtain the dynamical Lorentzian relaxation function $G^{\rm DL}(t;a,H_{\rm LF},\nu)$.

In this picture, a weighting function $\rho_a(\Delta)$ was introduced to sum up the contributions from every muon sites (see eq.29). In real spin systems, the upper bound of the site-sum integral should be replaced by a cut-off field $\Delta_{\rm max}$:

where $\rho_a'(\Delta)$ is normalized for the new upper bound $\Delta_{\rm max}$:

The physical meaning of the cut-off field $\Delta_{\rm max}$ is the largest possible Gaussian field width for the dilute spin system considered. This quantity may be of the same order of magnitude as the hypothetical Gaussian width ($\Delta_{100\%}$), which is expected when all the lattice points are filled up with moments. Since the relation between $\Delta_{100\%}$ and the Lorentzian width (a) has been obtained (eq.26), $\Delta_{\rm max}$ is estimated to be:

where c is the dilute spin concentration and a is the Lorentzian width.

  

Figure 22: $\Delta_{\rm max}$-corrected Lorentzian relaxation function for $\Delta_{\rm max}/a=20$ (solid lines). The dotted lines are square-root exponential functions ($\exp(-\sqrt{\lambda t})$), which is realized in the ideal Lorentzian field distribution.

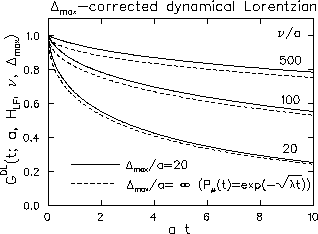
The most significant correction because of the cut-off field $\Delta_{\rm max}$ appears in the fast fluctuation regime. In the traditional Lorentzian theory, the relaxation function in this regime is a square-root exponential function (eq.32). When the cut-off field is introduced, the relaxation at large fluctuation rates loses the fast front-end of the square-root exponential behavior, because the fast front-end originates from the T₁ relaxation of muons which locate at sites with large local fields. In Fig.22, the $\Delta_{\rm max}$-corrected dynamical Lorentzian functions [$G^{\rm DL}(t;a,H_{\rm LF},\nu,\Delta_{\rm max})$] are compared with the square-root exponential functions of the ideal case.

The $\Delta_{\rm max}$-corrected dynamical Lorentzian function is well approximated by a `stretched' exponential function, $\exp(-(\lambda t)^\beta)$; in Fig.23, the stretching power ($\beta$) is shown as a function of the normalized fluctuation rate ($\nu/a$). At small fluctuation rates, the power converges to 1/2, as expected for the square-root exponential behavior, and in the large fluctuation limit, $\beta$ approaches 1.

  

Figure 23: Stretching power $\beta$ derived from the stretched exponential function fit to the $\Delta_{\rm max}$ corrected relaxation function.

Experimentally, muon spin relaxation in paramagnetic dilute spin systems often exhibits a stretched exponential behavior, with its power $\beta$ approaching 1 at high temperatures [40]. The above mentioned cut-off field effect may explain at least part of the phenomena.